Introducere – de ce avem nevoie de limbaj formal în matematică?
Matematica este cunoscută ca fiind singura disciplină care poate oferi demonstrații ultime pentru realitățile pe care le descrie, rigoarea și exactitatea fiind intrinseci demersului matematic. Demonstrațiile matematice sunt văzute ca dovezi infailibile pentru adevăr sau falsitate, matematicienii căutând mereu demonstrații riguroase pentru a stabili o dată pentru totdeauna validitatea sau invaliditatea afirmațiilor pe care le studiază. Cu toate acestea, matematica are o problemă serioasă la acest capitol: s-a demonstrat, și încă riguros, formal, că există afirmații adevărate, dar care nu pot fi demonstrate în această manieră formală, puterea limbajului matematic fiind limitată la descoperirea unui adevăr parțial. Acest rezultat, cu ecouri în concepția modernă despre cunoașterea științifică, a fost formulat de matematicianul austriac Kurt Gödel sub forma Teoremelor de incompletitudine, despre care voi vorbi în acest articol.
Pentru început, îmi propun să prezint succint fundamentele logicii formale, cea mai abstractă, dar și cea mai exactă parte a matematicii, un adevărat pilon pe care este construit – într-o manieră mai mult sau mai puțin explicită – întreg edificiul matematic modern pe care umanitatea l-a articulat. Dat fiind că înțelegerea ideii de demonstrabilitate riguroasă prezentă în teoremele lui Gödel necesită anumite noțiuni de logică formală, voi trece în revistă structura și funcționarea acestui tip limbaj, dar și anumite limitări pe care acesta le impune sau care intervin ulterior din folosirea lui. Acest preambul îmi va permite să discut o formă simplificată a primei teoreme de incompletitudine a lui Gödel, care demonstrează că limbajul formal începe să șovăie în momentul în care încercăm să formalizăm chiar și cel mai simplu sistem infinit, cum sunt numerele naturale.
Mai întâi, însă, să vedem de ce matematica are nevoie de limbaj formal. Demersul matematic se diferențiază de cel propriu altor științe prin faptul că, în calitate de matematician:
1. Poți defini obiecte noi, în sensul în care nu există o clasă finită, prestabilită, de obiecte cu care poți lucra. Îți poți crea propria „realitate matematică”, atât timp cât demonstrezi că poate exista.
2. Această creație nu se poate face chiar oricum. Spre exemplu, este evident pentru oricine că nu putem defini mulțimea numerelor care sunt, spre exemplu, frumoase. Definiția este subiectivă și prea vagă pentru a fi considerată matematică.
Exemplul „numerelor frumoase” este unul extrem, însă, avansând în matematică, vedem că distincția între o definiție matematică și una inacceptabilă din punct de vedere matematic este mult mai fină. Să luăm, spre exemplu, o noțiune pe care mari matematicieni, precum Leibniz, Newton și alții nu au exprimat-o riguros în lucrările lor, anume noțiunea de funcție continuă. Aceștia au scris adevărate tratate de Analiză Matematică, fără a avea o definiție formală a ce înseamnă o funcție continuă: pentru ei, o funcție continuă însemna, mai mult sau mai puțin, o linie curbă neîntreruptă, desenată fără a ridica creionul de pe hârtie. Exprimare pur intuitivă, care funcționează în cazurile simple întâlnite în problemele din matematica și fizica acelor vremuri, dar care începe să nu mai fie suficientă în momentul în care dorim precizie în exprimare.
De pildă, cu această definiție intuitivă, e greu de crezut că există o linie curbă continuă care oscilează de o infinitate de ori pe porțiuni oricât de mici – un fel de zigzag oricât de fin, ca în imaginea de mai jos:
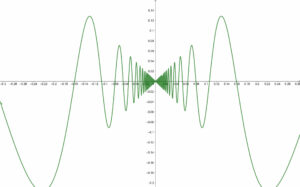
Cu toate acestea, aplicarea definiției formale a funcției continue, introdusă la începutul secolului al XIX-lea de către Augustin Louis Cauchy, permite demonstrarea existenței unor astfel de curbe continue neobișnuite.
Astfel de cazuri care stau la limita intuiției ilustrează necesitatea logicii formale, ce reprezintă un sistem bine determinat de combinații de simboluri admisibile. Aceste combinații poartă numele de formule logice și sunt singurele entități pe care ne dăm voie să le utilizăm în definirea conceptelor matematice și a exprimării relațiilor dintre ele1.
Înainte de a intra efectiv în studiul acestor formule, trebuie să subliniez meritul unor personalități renumite din matematică, precum David Hilbert și Bertrand Russel, care au contribuit decisiv la implementarea sistemului logicii formale. La începutul secolului al XX-lea, David Hilbert propune un program de formalizare absolută a întregii matematici cunoscute până la acea vreme, evidențiind necesitatea unei abordări riguroase prin formule clare, cu metode de deducție bine stabilite. Acesta visa la o matematică sprijinită temeinic pe sisteme de axiome ce nu se contrazic reciproc și care pot demonstra adevărul sau falsitatea oricărei afirmații formalizate în limbajul lor. Urmând aceeași linie de gândire ca David Hilbert, Bertrand Russel scrie, împreună cu Alfred North Whitehead, o monumentală lucrare în trei volume intitulată Principia Mathematica (1910 – 1913), în care, printre altele, dă formă imbajului logicii matematice și metodelor de demonstrație extrem de riguroase, pe baza cărora matematicienii vor încerca ulterior să facă din dorința lui David Hilbert o realitate.
După cum vom vedea, însă, acestă dorință a rămas doar un vis, spulberat de către Kurt Gödel câteva decenii mai târziu, în 1931, prin Teoremele de incompletitudine, acestea demonstrând – riguros, în logica formală introdusă în „Principia Mathematica” – faptul că demersul de a axiomatiza matematica într-o manieră completă nu este posibil nici măcar în cazul aparent simplu al numerelor naturale.
Limbajul formal
Vom trece acum la prezentarea pe scurt a modului efectiv în care operează logica formală. Avem de a face cu un limbaj compus din anumite simboluri admisibile – funcția lor nu diferă foarte mult de cea a literelor alfabetului, ce creează cuvintele și propozițiile limbajului natural. În prezentarea noastră, vom folosi următoarele simboluri:
\[ (\text{ }) \neg \wedge \vee \Rightarrow \Leftrightarrow \forall\hspace{0.1cm} \exists =\]
pe lângă litere ce vor exprima numere naturale oarecare. Simbolurile de mai sus reprezintă (în ordine) paranteze, semnul de negație, ȘI, SAU, implicație, echivalență, cuantificatorul universal (tradus prin „pentru orice”), cuantificatorul existențial („există”) și semnul egal. Aceste simboluri sunt combinate într-o manieră clar stabilită, pentru a crea formule ce au sens din punct de vedere logic.
Un exemplu de formulă scrisă în acest limbaj este:
\[ x \wedge y,\]
ce se traduce „x ȘI y”. Un alt exemplu, ceva mai elaborat, ar putea fi
\[ (\forall x) (x=y\vee x=C), \]
adică, „orice x este egal cu y sau este egal cu C”. Trebuie remarcat, însă, că anumite expresii formate cu aceste simboluri nu pot avea sens. Spre exemplu,
\[ x\wedge \vee = \]
s-ar traduce prin „x ȘI SAU EGAL”, ceea ce evident nu exprimă nimic inteligibil.
Demonstrații și demonstrabilitate
Până acum ne-am preocupat de structura limbajului logic. Vom vedea în ceea ce urmează cum putem pune în aplicare formalismul introdus mai sus pentru a face cel mai riguros – dar și cel mai abstract – tip de demonstrații matematice: demonstrațiile formale.
Pentru început, considerăm o colecție de formule, numite axiome, care sunt punctul de plecare al oricărei demonstrații. Acestea cuantifică proprietăți logice de bază, ce provin dintr-o evidență intuitivă. Un prim exemplu de axiomă exprimă faptul absolut evident conform căruia, dacă două formule sunt adevărate, atunci prima formulă este adevărată. Formal, aceasta se scrie
\[ F\Rightarrow (G\Rightarrow F),\]
unde F și G pot fi orice formule (valide).
Până aici nu putem vorbi despre demonstrații, dat fiind că nu avem o regulă de generare a unor noi formule adevărate, pe baza axiomelor. Avem nevoie de așa numitele reguli de deducție, care, la fel ca axiomele, ilustrează intuiții logice primare. Dintre cele două reguli de deducție din logica formală, o voi ilustra pe cea numită Modus Ponens. Intuitiv, dacă o formulă este adevărată, iar altă formulă este o consecință a celei dintâi, atunci a doua formulă este adevărată. Formal, avem:
Din \( F \) și \( (F\Rightarrow G) \) adevărate, deducem \( G \) adevărată
A demonstra că o formulă2 este adevărată revine la a găsi un șir finit de formule ce se încheie cu formula de demonstrat, astfel încât fiecare dintre componentele înșiruirii ori este o axiomă, ori poate fi generată printr-un procedeu de deducție permis, pornind de la formule ce există deja în șir. Cu alte cuvinte, șirul trebuie să conserve, din aproape în aproape, adevărul formulelor, fie prin faptul că axiomele sunt adevărate, fie prin faptul că regulile de deducție conduc la formule noi ce sunt adevărate.
Concluzie parțială
Până acum, am prezentat ce înseamnă ca o formulă să fie demonstrabilă formal, pornind de la un sistem de axiome prestabilit. În continuare, mă voi concentra pe axiomatizarea numerelor naturale, încheind expunerea cu o formă simplificată a primei teoreme de incompletitudine a lui Kurt Gödel, ce afirmă incapacitatea demonstrației formale de a surprinde toate adevărurile privitoare la mulțimea numerelor naturale.
Axiomatizarea numerelor naturale – Axiomele lui Peano
Pentru a putea înțelege la ce se referă exact Teoremele de incompletitudine ale lui Gödel, este nevoie, mai întâi, să vedem care sunt proprietățile esențiale pe care le au numerele naturale, proprietăți pe care vrem să le ilustrăm atunci când descriem numerele naturale în limbaj formal. Cea mai cunoscută astfel de axiomatizare a fost introdusă în secolul al XIX-lea de către matematicianul italian Giuseppe Peano.
În sistemul de axiome al lui Peano, un rol important îl joacă ideea de succesor. Fiecare număr natural admite în mod evident un număr imediat mai mare decât el: succesorul lui 0 este 1, al lui 1 este 2 și așa mai departe. Singurul număr natural care nu este succesorul unui alt număr natural este 0. Prima axiomă a lui Peano afirmă că un număr nu poate fi succesorul a două numere naturale diferite. Următoarele axiome cuantifică proprietățile de bază ale adunării, înmulțirii, ridicării la putere și a ordonării mulțimii numerelor naturale, care sunt evidente din punct de vedere intuitiv.
În final, un loc aparte în Axiomatica Peano îl are principiul inducției, ce permite demonstrarea proprietăților referitoare la numerele naturale din aproape în aproape. Să luăm, doar în scopuri ilustrative, o proprietate fictivă F(n): „numărul n este albastru”. Atunci, este la nivelul evidenței faptul că, dacă știm că:
I) numărul 0 este albastru și
II) în momentul în care un număr este albastru, atunci și succesorul lui este albastru,
atunci toate numerele vor fi albastre. De ce? Raționamentul decurge în felul următor: știm că 0 este albastru, deci, din proprietatea II), numărul 1 va fi albastru, fiind succesorul lui 0. În același mod, obținem că 2 este albastru, apoi 3 și așa mai departe, până când obținem că toate numerele naturale sunt albastre.
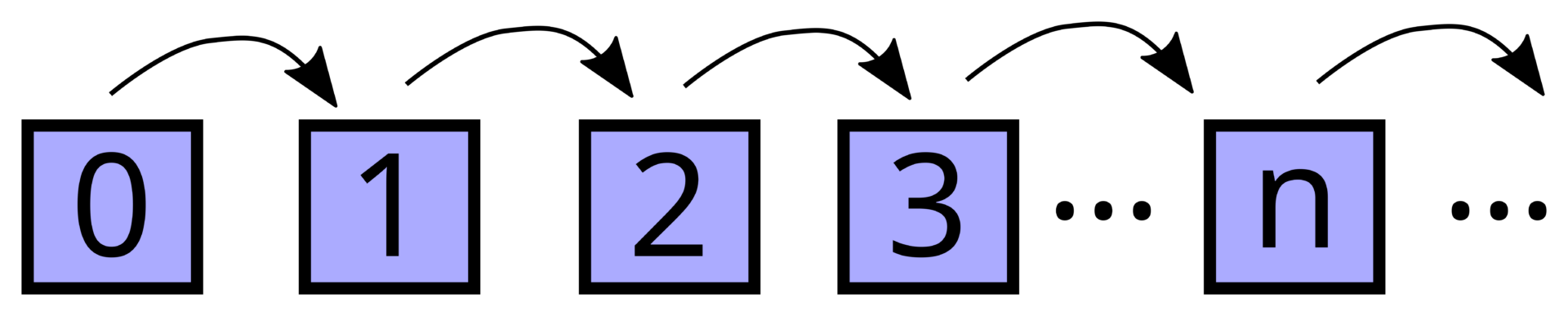
Formal, putem exprima acest procedeu în următorul fel: Pentru orice formulă F(n) ce se referă la un număr natural n oarecare3, următoarea afirmație este o axiomă: Dacă F(0) e adevărată și, pentru orice număr n, F(n+1) este o consecință a lui F(n), atunci F este valabilă pentru toate numerele naturale. La o primă vedere, avem de-a face cu aplicarea succesivă a regulii de deducție Modus Ponens. Totuși, dat fiind că orice demonstrație formală trebuie să aibă un număr finit de pași, nu putem proceda direct prin Modus Ponens, ci avem nevoie să introducem schema de axiome a inducției, formalizată astfel:
\[ F(0)\wedge (\forall n) (F(n)\Rightarrow F(n+1)) \Rightarrow (\forall n)(F(n)). \]
Remarcăm ceva esențial: limbajul formal pe care tocmai l-am introdus nu ne permite să scriem în simboluri următoarea cuantificare: „pentru orice formulă F are loc o proprietate”. Limbajul formal este astfel construit încât singurele obiecte după care putem cuantifica sunt cele la care se referă acesta, adică numerele naturale (exprimarea „orice număr natural satisface anumită proprietate” este singura utilizare permisă a cuantificatorului universal). Mai exact, \( (\forall F) \) nu este o expresie formală validă, deoarece limbajul nu operează pe mulțimea formulelor, pe când exprimarea \( (\forall n) \) este validă. Prin urmare, în cazul principiului inducției enunțat mai sus avem de a face cu o schemă de axiome, ce generează o axiomă distinctă pentru fiecare formulă particulară F(n). În niciun caz, nu putem scrie:
\[(\forall F) (F(0)\wedge (\forall n) (F(n)\Rightarrow F(n+1)) \Rightarrow (\forall n)(F(n))), \]
dat fiind că limbajul formal nu ne permite prima cunatificare. Pe parcursul secțiunilor următoare, vom vedea modalitatea prin care Kurt Gödel a reușit să evite această constrângere, în cadrul demonstrațiilor Teoremelor de incompletitudine și, în anumite circumstanțe particulare, să restrângă schema de axiome a inducției la o singură axiomă.
O variantă simplificată a primei teoreme de incompletitudine
Având această pregătire în minte, putem enunța o variantă simplificată a primei teoreme de incompletitudine:
Există o formulă referitoare la numerele naturale care este adevărată, dar care nu poate fi demonstrată formal.
Prin demonstrație formală înțelegem un șir finit de formule adevărate, ce pornește de la un sistem de axiome dat. Teoremă de incompletitudine de mai sus este adevărată în orice sistem de axiome în care avem proprietățile de bază ale operațiilor cu numere naturale și avem principiul inducției, adică un sistem de axiome4 care include Axiomele lui Peano. Ce înseamă acest lucru? Dacă dorim să formalizăm aritmetica numerelor naturale așa cum o cunoaștem (și așa cum o folosim în permanență), suntem condamnați la a avea adevăruri ce nu pot fi demonstrate formal, adică avem un sistem incomplet de cunoaștere.
Din culisele demonstrației
Una dintre cele mai ingenioase părți din demonstrația Teoremelor de incompletitudine este modalitatea prin care Kurt Gödel reușește să treacă peste limitările impusă de limbajul formal, anume imposibilitatea de a cuantifica după formule și imposibilitatea de a exprima demonstrabilitatea printr-o formulă. Așa cum am văzut în secțiunea despre inducție, putem scrie formal „orice număr natural are o proprietate”, dar nu și „orice formulă satisface o anumită proprietate”. Ideea ingenioasă a lui Gödel a fost aceea de a atribui fiecărui simbol câte un număr natural, apoi, prin alipirea acestor numere, fiecărei formule i se va asocia un unic număr natural. În final, orice șir finit de formule va avea atribuit un număr natural. De pildă, să pornim de la următoarea atribuire:
\[ \begin{array}{ccc}( & \to & 1 \\ ) & \to & 2 \\ = & \to & 3 \\ x & \to & 4 \\ y & \to & 5 \\ \forall & \to & 6 \end{array}\]
Atunci formula
\[(\forall x) (x=y) \]
va avea numărul Gödel 164214352, obținut prin alipirea numerelor asociate simbolurilor componente5. Cuantificarea după formule devine sinonimă cu cuantificarea după numere naturale, ce e posibilă în limbajul logicii formale. Astfel, schema de axiome a inducției devine o singură axiomă.
Mai mult, orice șir de formule ce formează o demonstrație formală poate fi acum exprimat printr-un număr Gödel6, conducând – după o demonstrație destul de complexă – la exprimarea demonstrabilității printr-o formulă. Mai precis, Gödel a arătat că există o formulă Dem(n) care este adevărată dacă și numai dacă n este numărul Gödel asociat unei formule demonstrabile formal. Prin urmare, demonstrabilitatea – care este o proprietate structurală, privitoare la existența unui șir de formule cu anumite proprietăți – este complet caracterizată de o formulă precisă.
Un rezultat complementar, ce se află în strânsă legătură cu demonstrația Teoremelor de incompletitudine, se referă la exprimarea adevărului prin expresii formale. Cunoscut sub numele de Teorema lui Tarski, acesta afirmă că nu există nicio formulă Adev(n) astfel încât Adev(n) este adevărată dacă și numai dacă n este numărul Gödel asociat unei formule adevărate referitoare la numerele naturale. Prin urmare, este demonstrat riguros faptul că, spre deosebire de demonstrabilitate, adevărul nu poate fi cuprins într-o exprimare formală.
Concluzie
Faptul că există proprietăți referitoare la cele mai simple obiecte matematice – numerele naturale – care sunt adevărate, dar nu sunt demonstrabile, ne arată o dată pentru totdeauna capacitatea limitată a rațiunii umane, ce operează secvențial, în cunoașterea legată de sisteme infinite. Deducțiile logice au un rol foarte important în dezvoltarea riguroasă a matematicii, dar este imposibil ca această contribuție să fie una ultimă. Rămâne deschisă întrebarea dacă putem ajunge cumva la cunoașterea acestor adevăruri care nu ne sunt accesibile prin gândirea formală, iar, dacă răspunsul este afirmativ, rămân de descoperit modalitățile prin care putem transcende această barieră a secvențialității, spre o viziune de ansamblu asupra adevărului.
NOTE
- O idee despre ce înseamnă, în primă instanță, această formalizare poate fi găsită și în articolul meu despre intuiție în matematică: De ce trebuie să fii om ca să faci matematică? ↑
- Riguros vorbind, nu putem aplica noțiunile de valoare de adevăr oricăror formule, ci doar acelora care nu au așa-numite variabile libere. În limbaj colocvial, formula F=„x este număr par” are o variabilă liberă, anume x, deoarece formula afirmă ceva despre x, o proprietate a lui x. Pe de altă parte, formula G=„orice număr natural x este par sau este mai mare decât 0” nu vorbește despre un x particular, ci vorbește, de fapt, despre toate numerele naturale, variabila x din formula G fiind doar o notație pentru un număr natural oarecare. Putem vedea clar că a doua formulă considerată (anume G) este adevărată, pe când valoarea de adevăr a formulei F depinde de alegerea lui x, fiind falsă pentru x=3 și adevărată pentru x=2. ↑
- Adică n este singura variabilă liberă din F. ↑
- (Recomand ca acestă notă să fie citită după parcurgerea întregului articol) Sistemele de axiome pentru care este valabilă Teorema de incompletitudine (varianta simplificată) nu pot fi oricât de generale, deoarece astfel am putea ajunge în situația de a crea un sistem ce conține ca axiome toate formulele adevărate referitoare la numerele naturale. Acest lucru nu este, însă, posibil, atâta vreme cât ne impunem ca sistemele de axiome să fie descrise într-o manieră algoritmică. Mai precis, în limbajul ultimei secțiuni a acestui articol, sistemul de axiome trebuie să fie descriptibil printr-o formulă Ax(n), ce este adevărată dacă și numai dacă n este numărul Gödel al unei axiome. În aceeași ultimă secțiune, am văzut că principiul inducției satisface această cerință, putând fi descris printr-o singură formulă, dar mulțimea tuturor formulelor adevărate nu poate fi descrisă printr-o formulă, conform Teoremei lui Tarski. Mai mult, adăugarea unui număr finit de axiome unui sistem nu alterează proprietatea acestuia de a fi descriptibil într-o manieră algoritmică. ↑
- De fapt, având în vedere că putem avea formule cu un număr oricât de mare de variabile, nu doar două: x și y, procedăm în felul următor: considerăm variabilele ca formând un șir \( x_1, x_2, x_3\ldots \), iar pentru fiecare variabilă \( x_n \) asociem un număr Gödel format de numărul asociat simbolului x (adică 4) urmat de un alt număr, neasociat niciunui simbol, spre exemplu 7. Astfel, numărul Gödel al variabilei \( x_3 \) va fi 4777. ↑
- Formulele din șir vor fi separate printr-un alt număr (de pildă, 8), ce marchează trecerea de la o formulă la următoarea. ↑
Le mulțumesc colegilor mei Andrei Cațaron și Horațiu Cheval de la Facultatea de Matematică și Informatică, Universitatea din București, pentru sugestille privind conținutul articolului.
Sursă imagine: Unsplash

