Syntopic

Când, la începutul secolului XX, David Hilbert inițiază celebrul său program de formalizare a matematicii, această disciplină intră într-o nouă epocă, luând un avânt imens mișcarea formalistă ce dorea crearea unei matematici pur simbolice și rupte de realitatea lumii, cu scopul de a-i spori rigoarea. Dacă, în secolele trecute, matematicienii erau oameni care studiau diferite fenomene naturale, elaborând un formalism împletit de multe ori cu intuiția, David Hilbert vede matematica modernă ca pe un sistem închis, autosuficient, care își validează propriile rezultate bazându-se pe axiome ce pot fi, la o adică, doar niște formule alese arbitrar, fără a avea în spate vreo realitate. Acest curent formalist pierde din vedere exact latura umană a matematicii, acea sclipire de gândire creativă și imaginativă ce nu poate fi imitată de sistemele formale, oricât de sofisticat ar fi construite.

Matematicienii – mașini de calcul simbolic?

Concepția formalistă prezentată mai sus se poate rezuma astfel: există un set de simboluri ce se vrea a fi manipulat, simboluri ce sunt golite de orice semnificație. Astfel, cifra 2 ar putea fi înlocuită de un 🙂 și cifra 3 de un 🙁 fără a altera cu nimic discursul matematic. Apoi, există așa-numitele axiome – înșiruiri arbitrare de simboluri fixate anterior – și anumite metode permise de manipulare a simbolurilor. Spre exemplu, să considerăm banalul 2+3=5. O operație permisă este, de pildă, transformarea acestei expresii în 2=5-3. Pentru un formalist, acest demers nu diferă deloc de cel în care avem înșiruirea acceptată a priori: 🙂 * 🙁 ~ 😉 și transformarea permisă prin care T₁ * T₂ ~ T₃ se poate transforma în T₁ ~ T₃ $ T₂, aplicabilă pentru orice simboluri sau grupe de simboluri reprezentate de T₁, T₂ și T₃. În acest mod pur formal, operațiunea firească prin care 2+3=5 devine 2=5-3 este analogul transformării expresiei 🙂 * 🙁 ~ 😉 în 🙂 ~ 😉 $ 🙁 , fără ca semnificația intuitivă (două, trei obiecte etc.) să aibă vreo relevanță. În acest context lipsit de orice intuiție, matematicianul devine o mașinărie de calcul simbolic (manipulare de simboluri după anumite reguli precise).

Cum ar arăta, în această paradigmă, învățarea matematicii, rezolvarea de probleme și, mai general, întreaga cercetare matematică? În primă fază, elevii și studenții fac cunoștință cu simbolurile ce apar în discursul matematic, apoi cu operațiile permise ce se pot efectua cu acestea. A doua fază este cea a învățării a cât mai multe succesiuni de pași permiși, ce conduc de la un șir de simboluri (enunțul unei probleme) la alt șir de simboluri (soluția problemei), acest din urmă șir având o anumită structură dorită. Ultima fază – în care se încadrează inclusiv cercetarea la orice nivel în matematică – este cea a rezolvării de probleme noi. Pentru un formalist, rezolvarea problemelor constă în alegerea unei probleme (un șir inițial de simboluri reprezentând enunțul și un șir final de simboluri reprezentând forma scontată a soluției), apoi parcurgerea mentală, recurgând la memorie și la experiență, a tuturor succesiunilor de pași pe care cercetătorul le-a întâlnit anterior și încercarea de a aplica aceste scheme în speranța obținerii formei finale dorite. Urmează publicarea rezultatului în același formalism unanim acceptat.

Pașii descriși mai sus pot fi simulați de către un calculator suficient de performant, în care au fost adăugate suficiente succesiuni de pași astfel ca, mai mult sau mai puțin din întâmplare, acesta să transforme șirurile-enunț în șirurile-soluție pentru anumite categorii de probleme. Ceea ce lipsește în tot acest peisaj este înțelegerea realităților ce stau în spatele simbolurilor, vederea sensului ce nu poate fi cuprins în formalism. Și nu mă refer aici doar la anumite obiecte și procese fizice modelate matematic, ci și la unele descrieri, care, deși abstracte, țin totuși de acel tip de intuiție cu totul propriu matematicii, aspect pe care îl voi studia în detaliu mai jos.

Ce face ca matematica să fie umană?

Sau, mai exact, unde se află contactul dintre simbolurile formale și lume? Răspunsul simplu și imediat este: în crearea axiomelor. În geometrie, „o dreaptă e unic determinată de două puncte distincte” e o axiomă pentru că oamenii au avut de-a face cu obiecte ce sunt lungi și subțiri și trec prin două puncte – spre exemplu, un cablu întins între doi stâlpi. De aici, matematica se ocupă formal de tot, nemaifiind nevoie de nicio intervenție pur umană, ci doar de manipulări de simboluri ca cele descrise mai sus.

Răspunsul simplu și imediat nu este însă și complet, deoarece acesta ignoră faptul că mintea percepe obiectele matematice ca fiind realități la limita dintre concret și abstract, realități ce acționează unele asupra altora într-o ordine ce nu poate fi captată de formalismul pur. Acestă percepție a ordinii – care uneori uimește prin frumusețe – se situează deja în registrul intuiției care, fie și matematică, poate fi doar a unei persoane.

Voi ilustra la ce mă refer prin următorul exemplu. Definiția formală a unei funcții continue este o înșiruire de simboluri, pe care, pentru efectul pur ilustrativ, o voi include aici:

\[ (\forall) \varepsilon >0 (\exists) \delta_\varepsilon >0, \text{ }\forall y\in (x-\delta_\varepsilon,x+\delta_\varepsilon),\text{ } |f(x)-f(y)|<\varepsilon \]

Luată ca atare, această definiție este greu de pătruns, deci și de manipulat în rezolvarea de probleme. O schimbare de perspectivă, însă, ne permite să vedem funcția ca pe o curbă neîntreruptă (continuă) în plan. Astfel, definiția capătă o interpretare geometrică, încă abstractă, dar ușor manipulabilă prin gândirea intuitivă. Asocierea dintre funcție și curba plană din imaginea de mai jos face ca anumite afirmații să fie evidente, fără formalizări suplimentare. Aceste evidențe preîntâmpină calculul formal și îl validează intuitiv. Spre exemplu, putem intui „cu certitudine” faptul că, dacă această curbă se află și de o parte și de alta a unei linii drepte, atunci ea va intersecta acea linie (ca în figura de mai jos), fapt greu de dedus – dacă nu imposibil fără ajutorul intuiției – prin calcul formal pornind de la definiția de mai sus.

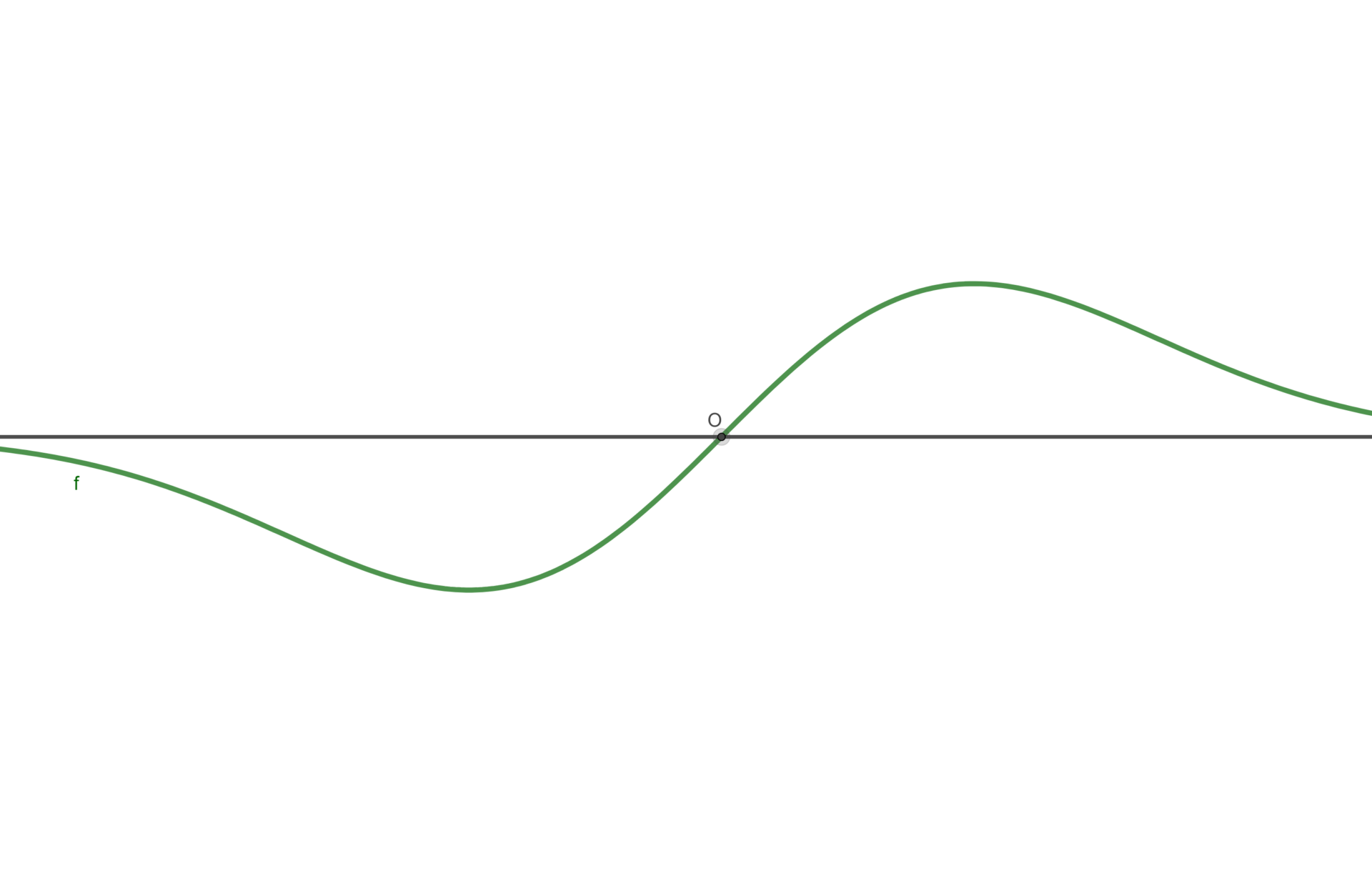
Prin urmare, intuirea semnificației conceptului cu care lucrăm conduce nu doar la alegerea unor axiome potrivite, ci și la deducerea unor proprietăți pe care obiectul „este evident că le are”, fiind, de asemenea, sugerată și metoda formală (succesiunea de pași) potrivită pentru demonstrarea riguroasă a rezultatului. În exemplul de mai sus, ideea unei curbe neîntrerupte determină, pe de o parte, definiția formală din expresia simbolică și, pe de altă parte, conduce la intuirea și demonstrarea rezultatului dorit, acela că graficul funcției (curba) intersectează linia dreaptă. Astfel, intuiția nu înlocuiește formalismul, dar îl direcționează și îi atribuie sens.

Diverse forme ale intuiției – la intersecția dintre abstract și concret

Multe din formele intuiției matematice țin de lumea fizică, obiectele matematice fiind modele pentru anumite fenomene dinamice sau transformări (dilatări, rotații) ale planului sau spațiului. Altele, precum exemplul curbei continue, sunt interpretări geometrice, reprezentări grafice ale proprietăților definitorii ale elementelor matematice.

Există, însă, și intuiții interne ale matematicii, mai complexe, date de interacțiunea reciprocă a elementelor matematice, care nu au corespondent imediat în lumea reală. Acest al doilea tip de intuiții scot matematica din sfera empirică, creând un limbaj intuitiv propriu ei, care, deși conține multe analogii cu procese din realitate, se referă totuși la interacțiuni abstracte între obiecte abstracte. Astfel, matematicianul nu este un empirist, ci este o persoană care își folosește imaginația pentru a-și crea un univers coerent, abstract, în mintea sa, pe care apoi să îl manipuleze cu ajutorul gândirii.

Un exemplu simplu ar fi cel al transformărilor planului (translații, dilatări etc.) care acționează asupra formelor geometrice – obiecte abstracte ale gândirii – într-o manieră descriptibilă prin cuvinte din limbajul uzual: O translație deplasează un triunghi într-o anumită direcție. O rotație învârte planul cu 30 de grade ș.a. Cu toate că acest exemplu ține, mai degrabă, de intuiția fizică a obiectelor matematice, el poate da o idee despre limbajul intuitiv pur matematic care, cu toate că folosește cuvinte uzuale, reprezintă realități extrem de abstracte¹.

Intuiția nu e același lucru cu simțul comun

Toate beneficiile intuiției, enunțate mai sus, ascund totuși în spate un pericol, acela al evidenței fără demonstrație. Procedând doar intuitiv în cunoașterea matematică, ne putem confrunta cu exact acele contradicții care au dus la consolidarea limbajului formal și la impunerea rigorii ce caracterizează întreg edificiul matematic. Un exemplu edificator este reprezentat de teoria numerelor cardinale, studiată pe larg în articolul Câteva intuiții matematice pentru noțiuni teologice (partea I). În cadrul acestei teorii, un prim paradox contrar intuiției este faptul că mulțimea numerelor naturale {0,1,2,3,…} și mulțimea numerelor întregi {…,-3,-2,-1,0,1,2,3,…} au același număr de elemente. Chiar dacă bunul simț ne spune că a doua mulțime trebuie să fie mai mare, o persoană familiară cu domeniul are intuiția clară a egalității celor două cantități. În astfel de cazuri, rolul experienței și a cunoașteri în profunzime a disciplinei studiate nu este acela de a oferi scheme de gândire, ci de a rafina intuițiile, mintea căpătând facultatea de a manipula corect în modul intuitiv obiectele matematice cu care operează, sincronizând evidențele cu rezultatele demonstrabile formal. Spre exemplu, pentru un matematician cu experiență devine evident faptul că numerele naturale sunt la fel de numeroase ca numerele întregi, iar negarea acestui fapt se situează deja în sfera nonsensului – nu doar formal, ci și intuitiv.

În final, în aceeași manieră în care corpul fără suflet e mort, nu putem priva matematica de componenta umană, intuitivă, de profunzime, astfel rămânând doar în sfera formulelor formale. Pe de altă parte, o intuiție fără argumentare formală riguroasă nu poate constitui cunoaștere matematică, formalismul fiind cel care susține și validează ultim rezultatele intuite.

NOTE

1. Pentru cititorul mai avansat, voi da astfel de exemple de intuiții abstracte: un operator ce acționează asupra unei funcții, o familie abstractă de mulțimi care acoperă o altă mulțime, un șir convergent sau o funcție continuă într-un spațiu topologic abstract. ↑

Imagine: Unsplash