Syntopic

În acest articol voi prezenta unul dintre cele mai întâlnite instrumente folosite în studiile științifice, atât în domeniul științelor naturii, cât mai ales în cele sociale. Este vorba despre verificarea ipotezelor din punct de vedere statistic, abordând în mod special acei indicatori care fac diferențierea dintre un rezultat valid și unul neconcludent din punct de vedere statistic. Dat fiind că manipularea rezultatelor studiilor statistice este una dintre preocupările principale ale promotorilor curentelor scientiste, consider că o cunoaștere a noțiunilor de bază despre relevanța statistică constituie una dintre modalitățile eficace prin care ne putem feri de falsa „știință”.

Voi începe cu o situație familiară tuturor, aceea a statisticilor medicale cu privire la pandemie. Un exemplu simplist (și fictiv) este următorul: dorim să studiem dacă vaccinarea scade riscul îmbolnăvirii cu COVID-19. Cum procedăm? Alegem 2000 de persoane, aparținând grupei de vârstă pe care dorim să o studiem, 1000 dintre ele fiind vaccinate și 1000 nevaccinate. Efectuăm teste zilnice și, la sfârșitul unei perioade de, să zicem, două săptămâni, numărăm cazurile pozitive din fiecare grup. Până aici totul este destul de clar. Partea delicată, care abia acum urmează, este interpretarea rezultatelor. Să presupunem că în grupul de persoane nevaccinate avem 300 de îmbolnăviri, iar în cel de persoane vaccinate avem 298 de îmbolnăviri. Este destul de limpede că rezultatul nu are cum să fie relevant, deoarece este evident o întâmplare faptul că avem cu două persoane bolnave mai puțin în cel de-al doilea grup. Prin urmare, acest studiu nu validează ipoteza „Vaccinarea reduce cazurile de îmbolnăvire”. Pe de altă parte, dacă am avea 300 de persoane bolnave în primul grup și numai 5 persoane bolnave în cel de-al doilea, putem, cu destulă încredere, să tragem concluzia că vaccinarea scade riscul de îmbolnăvire.

Exemplul de mai sus este unul extrem, în care concluzia se vede cu ochiul liber. Totuși, am vrea să cuantificăm într-un fel sau altul gradul de relevanță pe care un astfel de studiu îl are în validarea unei anumite ipoteze. Spre exemplu, ce am fi putut spune dacă în cel de-al doilea grup ar fi fost 270 de bolnavi? Care ar fi atunci probabilitatea să ne fi înșelat afirmând că vaccinarea reduce riscul de îmbolnăvire? Pentru a răspunde, vom pătrunde în teoria matematică a probabilităților, făcând cunoștință cu distribuțiile de probabilitate și cu noțiunile de medie și deviație standard. Toate acestea ne vor conduce la calcularea așa-numitelor valori Z și p asociate unui astfel de studiu statistic, cantități ce cunatifică gradul de relevanță al experimentului pentru validarea ipotezei studiate.

Distribuții de probabilitate

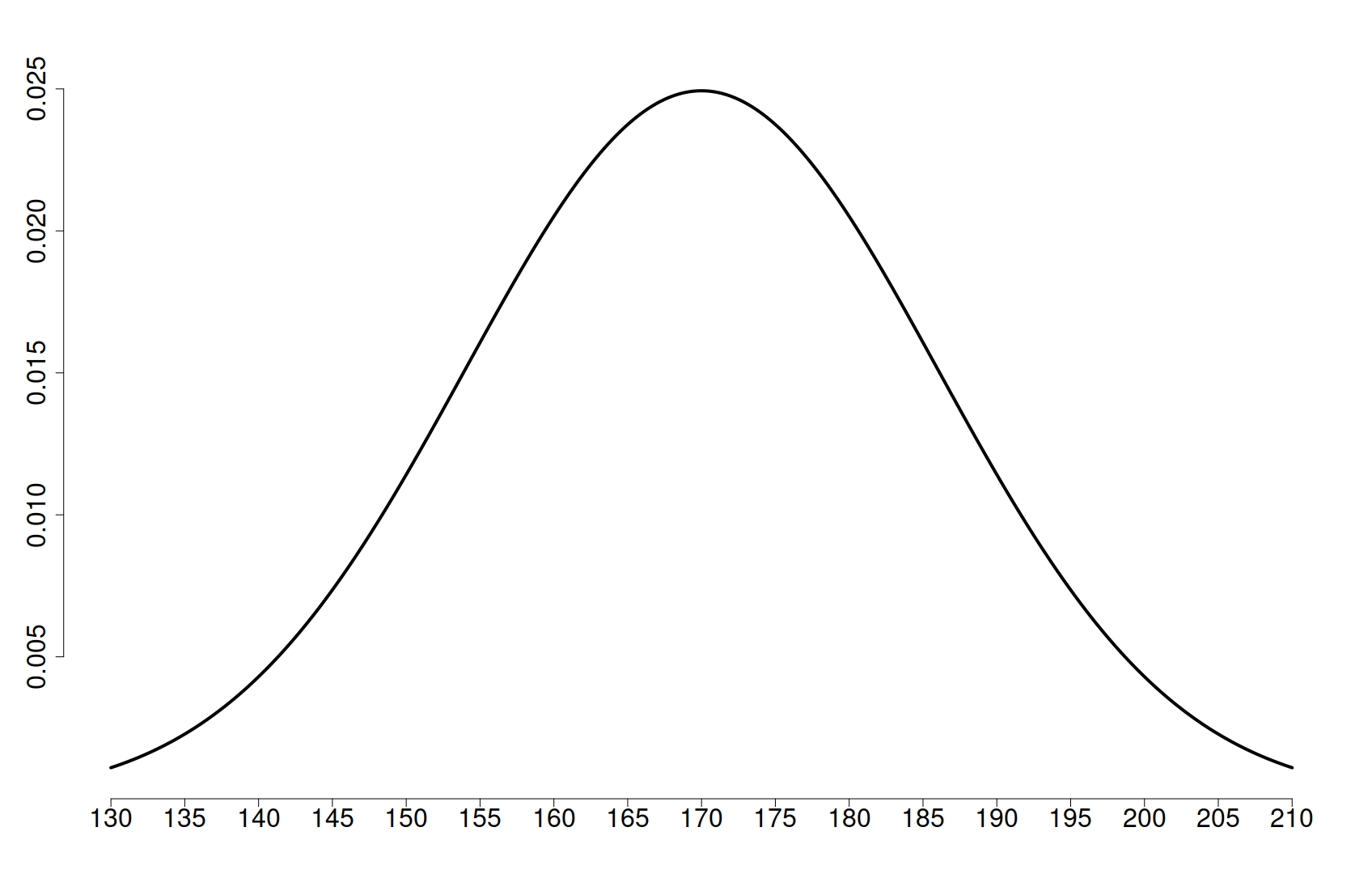
Nu toate fenomenele aleatorii din lumea înconjurătoare au același comportament. De pildă, aruncând o monedă, probabilitatea ca să apară una dintre fețe este egală cu probabilitatea să obținem fața opusă. Pe de altă parte, probabilitatea să petrecem mai puțin de o oră în sala de așteptare de la medic este considerabil mai mare față de probabilitatea de a petrece între 7 și 8 ore. Astfel, vedem că distribuția probabilistică a acestor fenomene e diferită, fapt care i-a condus pe matematicieni să definească așa numitele distribuții a probabilității. Știu, sună foarte complicat, dar totul se poate explica imediat cu ajutorul figurii de mai jos:

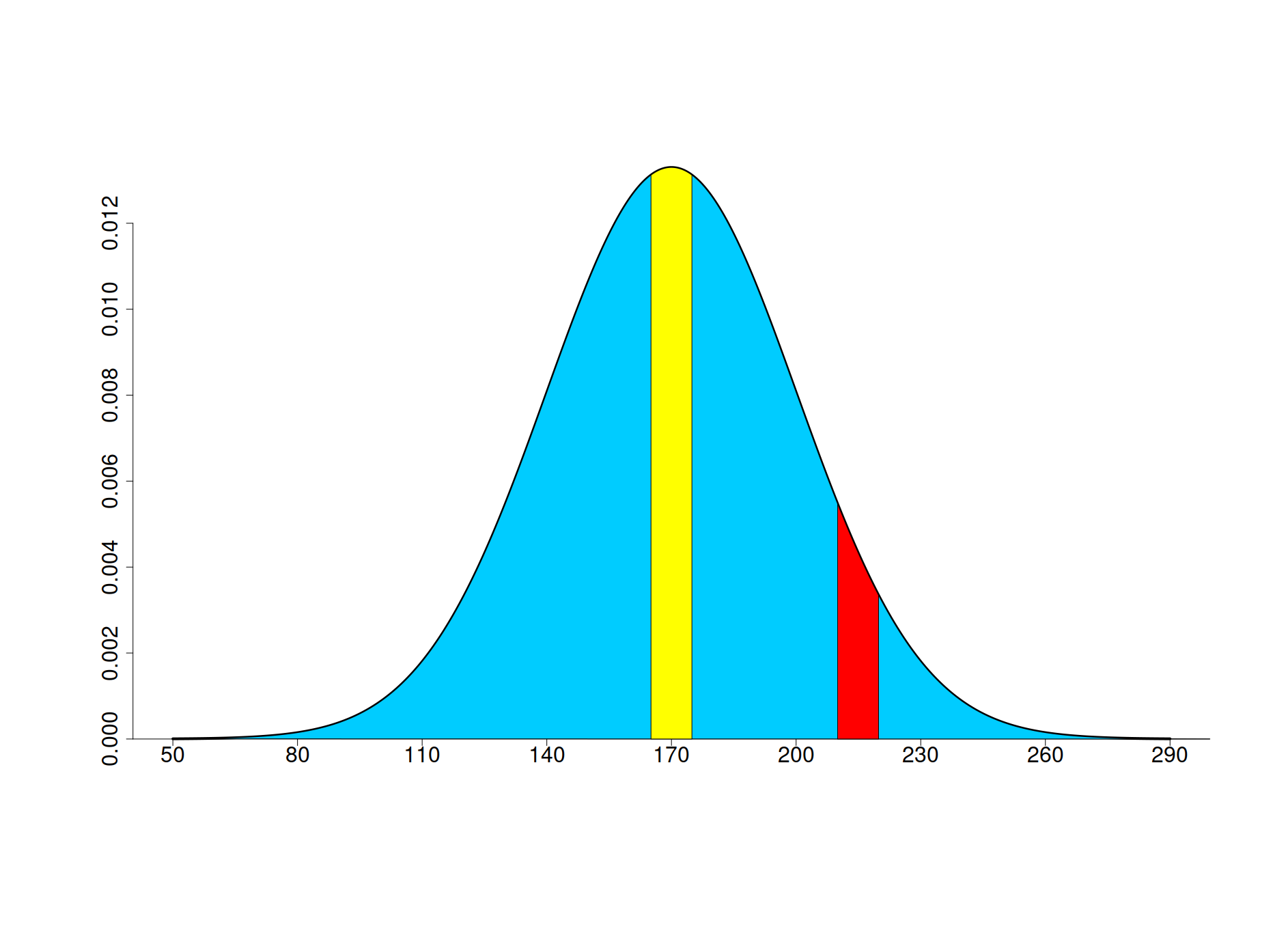
Graficul acesta reprezintă (din nou, datele sunt fictive) distribuția înălțimii într-o populație. Aria suprafeței marcate cu galben (având coordonatele orizontale între 165 și 175) reprezintă probabilitatea ca, alegând în mod arbitrar o persoană din populație, aceasta să aibă înălțimea între 165 cm și 175 cm. Porțiunea roșie (cu coordonate între 210 și 220) corespunde probabilității ca persoana să aibă între 210 cm și 220 cm. După cum se poate vedea, această a doua probabilitate este mult mai mică decât prima, ceea ce este de așteptat. În fine, aria totală – marcată cu albastru – este întotdeauna 1 (deci, maximă  – 100%) , adică probabilitatea ca înălțimea persoanei alese să aibă orice valoare.

Această distribuție se numește distribuție normală, ea fiind un model bun pentru caracteristici ce sunt influențate de foarte mulți factori și care variază în jurul unei valori medii, cum ar fi înălțimea sau greutatea multor indivizi de același sex și de aceeași vârstă. Un alt exemplu de valori distribuite normal sunt măsurătorile repetate – cu un anumit grad inevitabil de imprecizie – ale aceluiași obiect sau fenomen din fizică.

Următoarea întrebare pe care ne-o putem pune se referă la înălțimea „omului generic” din această populație, sau, cu alte cuvinte, care e cea mai întâlnită înălțime. Răspunsul este ușor de intuit în acest caz, fiind dat de valorarea înălțimii ce corespunde vârfului graficului, anume 170 cm. Prin urmare, este cel mai probabil să găsim persoane cu înălțimea în jurul valorii de 170 cm. Această valoare reprezintă media sau valoarea așteptată (în engleză expected value) a distribuției normale studiate.

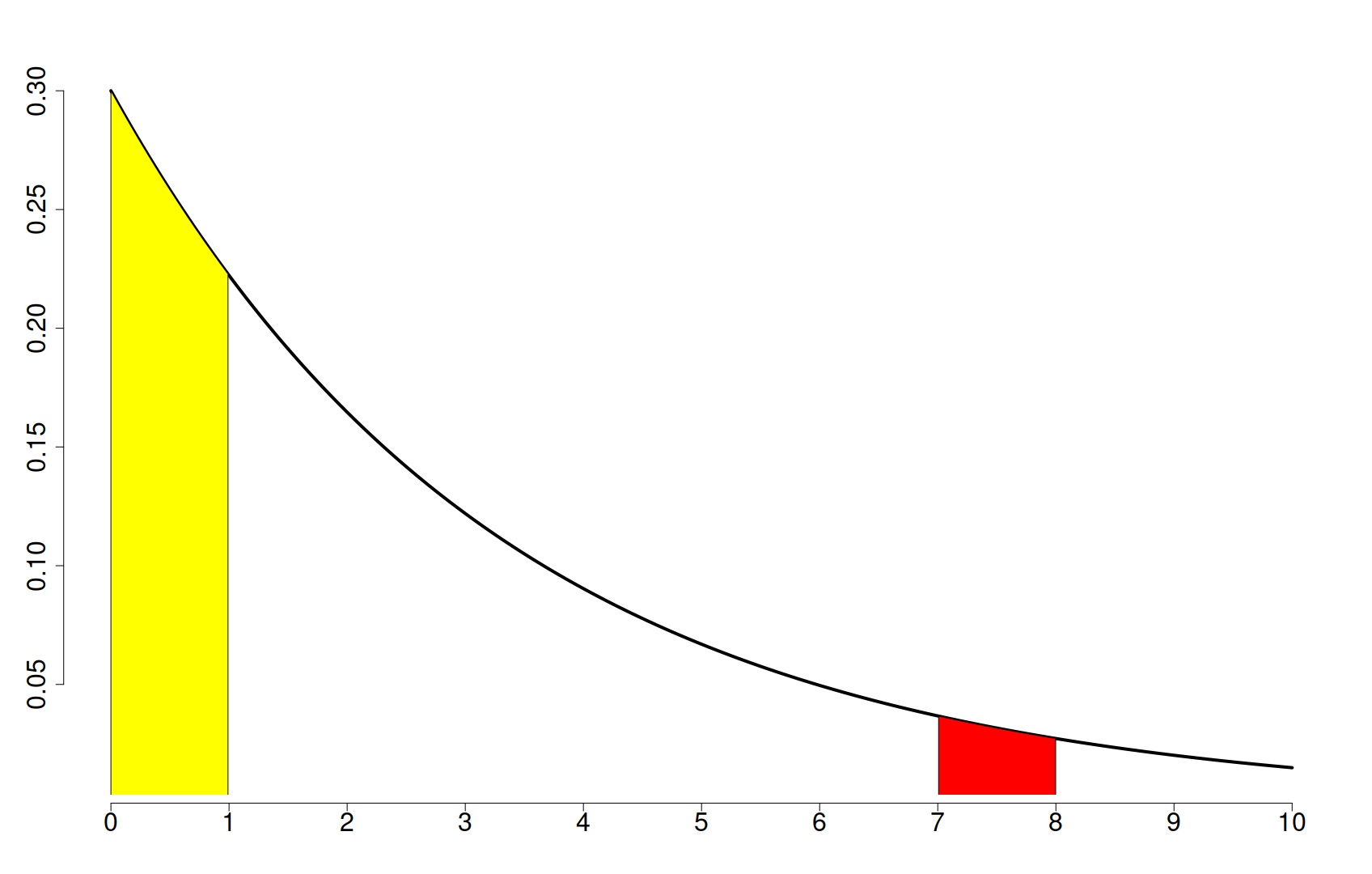
Graficul de mai jos descrie distribuția timpului de așteptare la medic, situație despre care discutam mai sus. Este clar că aria galbenă – corespunzătoare la 0-1 ore de așteptare – este mult mai mare decât cea roșie, corespunzătoare la 7-8 ore. Această distribuție de probabilitate, numită distribuție exponențială, corespunde mai bine intuiției cu privire la timpul de așteptare decât distribuția normală de mai sus.

Deviația standard

În continuare, dorim să studiem gradul de împrăștiere al valorilor unui proces aleator în jurul mediei. Cantitatea care cuantifică această împrăștiere se numește deviație standard. Spre exemplu, în cazul distribuției normale a înălțimii din Figura 1, cu cât deviația standard este mai mică, cu atât mai concentrate vor fi valorile în jurul mediei, adică foarte mulți indivizi vor avea înălțimi apropiate de media de 170 cm¹.

În cele două grafice de mai jos observăm două distribuții normale cu media 170, prima are deviația standard mică, iar a doua are deviația standard mai mare. Este mult mai probabil să întâlnim persoane înalte de aproximativ 150 cm în cel de-al doilea caz decât în primul.

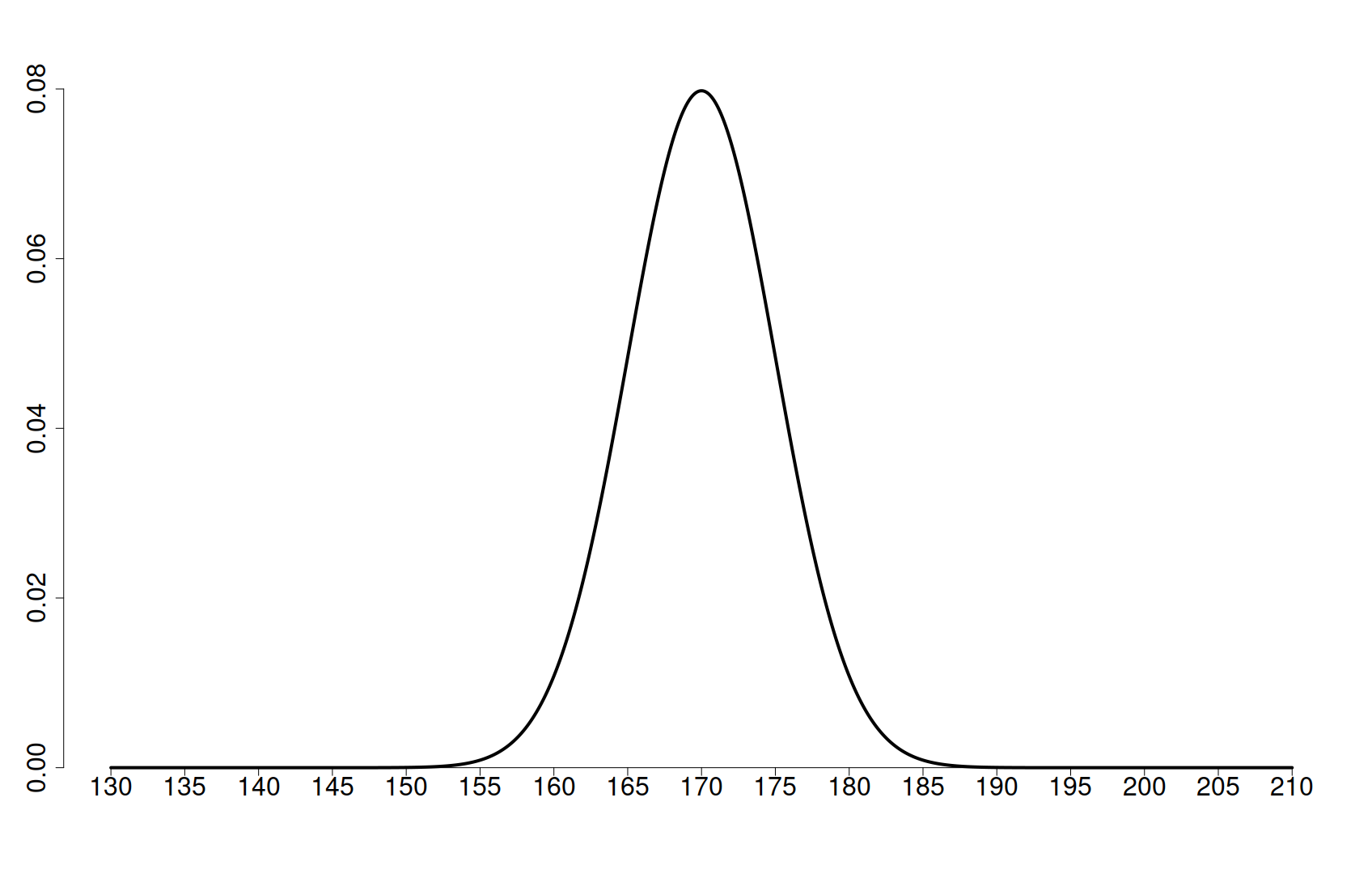
Mai merită subliniat faptul că o distribuție normală este pe deplin caracterizată de media și deviația sa standard. Media dă poziția vârfului clopotului, iar deviația standard caracterizează cât de larg sau îngust este acest grafic².

O teoremă esențială – Teorema limită centrală

Pentru a exprima rezultatul următor, este nevoie să considerăm un experiment, după cum urmează. Nu mai suntem interesați acum de înălțimea fiecărui individ, ci media de înălțime a unui grup de 5 persoane alese la întâmplare. Este firesc faptul că această valoare va fi tot în jurul înălțimii de 170 cm, având o oarecare distribuție de probabilitate. Tot intuitiv este și că, cu cât dimensiunea eșantionului este mai mare – să spunem 1000 în loc de 5 persoane – cu atât media înălțimilor eșantionului aleatoriu va fi mai concentrată în jurul mediei de 170 cm. Pur și simplu, șansa ca o înălțime mare să compenseze o înălțime mică în rândul celor 1000 de indivizi este mai mare decât în cazul a 5 oameni. Cu noțiunile de mai sus, media înălțimilor eșantionului de 1000 de persoane este distribuită conform unei distribuții de probabilitate cu valoarea așteptată 170 cm și deviația standard mai mică decât cea inițială (când ne interesa înălțimea individuală).

Acestea fiind zise, putem să considerăm diferența \( D=(\bar{h}-m) \) dintre media artimetică a înălțimilor unui eșantion de 1000 de indivizi și valoarea așteptată 170, care, la rândul ei va fi distribuită după o distribuție de probabilitate de medie 0 (ne așteptăm ca, scăzând 170 din toate înălțimile, să obținem valori concentrate în jurul lui 0).

Un rezultat fundamental în Teoria probabilităților, Teorema limită centrală, afirmă că, pentru un eșantion suficient de numeros, această diferență D este distribuită foarte apropape de o distribuție normală cu medie 0 și deviație standard mică. Fără a intra în detalii, teorema afirmă că, indiferent de distribuția inițială, dacă numărul de persoane n din eșantion este suficient de mare (spre exemplu 1000, în loc de 5), cantitatea

\[ Z=\sqrt{n}\frac{D}{s},\]

unde D este diferența de mai sus și s este deviația standard a populației, este distribuită după o distribuție normală de medie 0 și deviație standard 1³, a cărei grafic îl redăm mai jos:

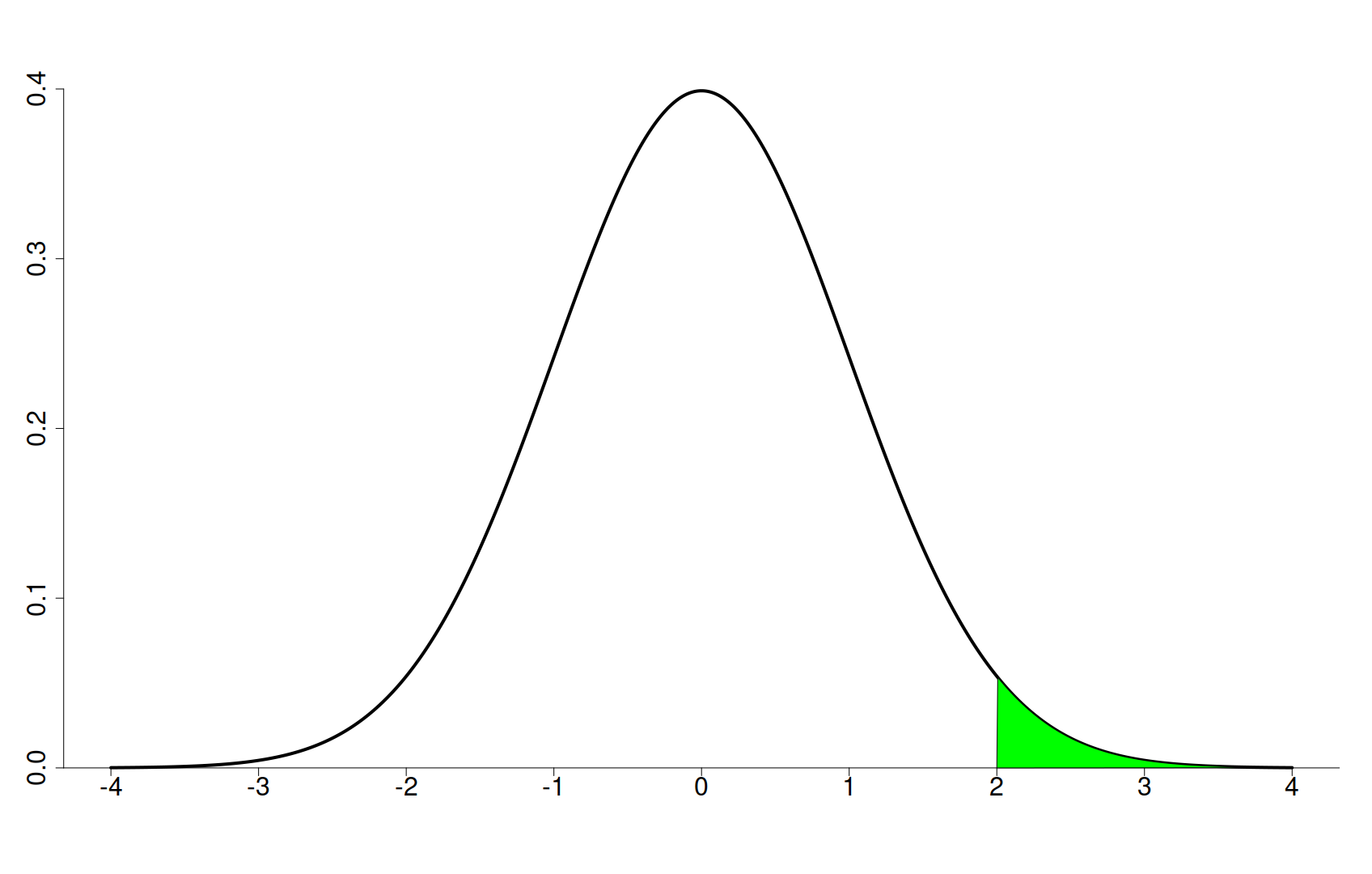
Cu alte cuvinte, teorema afirmă că, dacă sunt 1000 de persoane în eșantion și adunăm înălțimile lor, împărțim rezultatul la 1000 – până aici avem o medie aritmetică – scădem 170, apoi împărțim la deviația standard și rezultatul îl înmulțim cu \( \sqrt{1000}\simeq 31.622 \), rezultatul ne așteptăm să se afle undeva lângă 0. Mai mult, spre exemplu, probabilitatea ca acesta să fie mai mare decât 2 este destul de mică, fiind egală cu aria verde din Figura 4.

Ce relevanță are această construcție? Ea ne arată probabilitatea ca media unui eșantion să aibă o anumită valoare, atunci când atât valoarea așteptată a caracteristicii studiate (aici, înălțimea de 170 cm) la nivel de populație, cât și deviația standard sunt cunoscute.

Ne întoarcem la exemplul pandemic

Acestea fiind spuse, vrem să testăm ipoteza conform căreia vaccinul are efect în ceea ce privește numărul de îmbolnăviri, sau, mai exact, având anumite date empirice, vrem să știm care este probabilitatea de a ne înșela când facem această afirmație. Vom considera eșantioanele prezentate la începutul articolului, presupunem că lotul nevaccinat are 300 de îmbolnăviri, iar lotul vaccinat are 270 de îmbolnăviri.

Dacă lotul de test este bine ales, înseamnă că populația obișnuită, când nu este influențată de vreun medicament sau vaccin, are probabilitatea medie de îmbolnăvire de 300/1000, adică 30%. Ce ar rezulta din lipsa de efect a vaccinului asupra virusului? Faptul că probabilitatea medie de îmbolnăvire a lotului vaccinat ar fi tot 30%, adică îmbolnăvirile în rândul vaccinaților sunt distribuite conform acestui grafic:

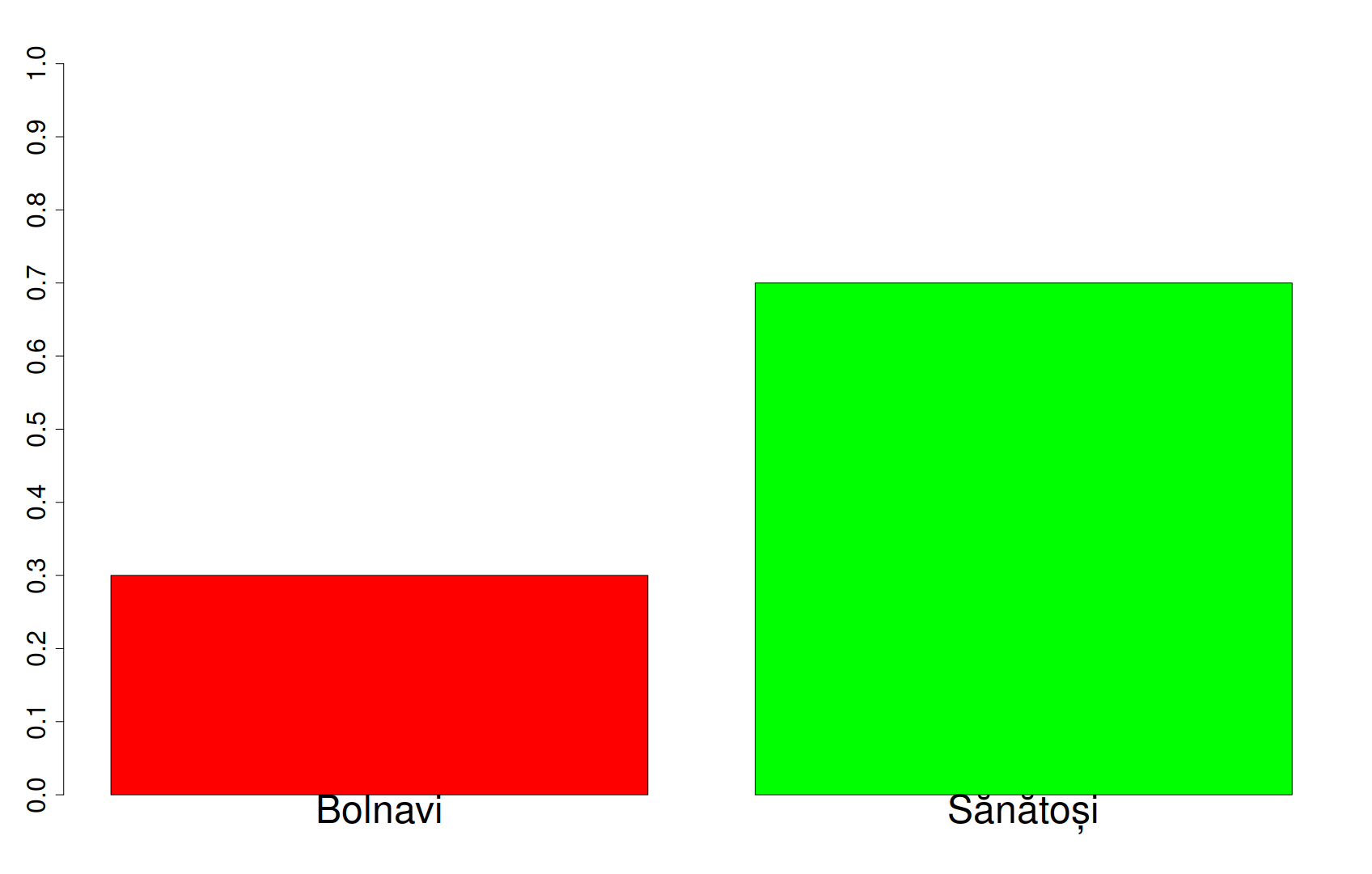
Ne interesează acum cât de probabil este ca, într-un eșantion de 1000 de oameni care au probabilitatea de îmbolnăvire presupusă de 30%, doar 270 de indivizi să se îmbolnăvească? Media eșantionului (emipirică) este deci, de 270/1000=27%.

Singurul ingredient care mai trebuie găsit pentru a putea aplica Teorema limită centrală este deviația standard. Pentru a nu îngreuna expunerea, voi scrie direct valoarea ei – egală cu 0,4582 – explicând într-o notă⁴ cum am ajuns la ea.

Următorul pas îl reprezintă calcularea valoari Z. Procedăm astfel: Media eșantionului vaccinat este 27%, iar media întregii populații este 30%. Scădem 27%-30%=-3%=-0,03. Împărțim la deviația standard și obținem -0,03/0,4582=-0,0654. Rezultatul îl înmulțim cu \( \sqrt{1000}\simeq 31,622 \), obținând -2,0680.

Prin urmare, probabilitatea să ne fi înșelat (cu alte cuvinte, chiar dacă valoarea așteptată este 30%, noi să obținem empiric cel mult 27%) este egală cu aria galbenă din figura de mai jos.

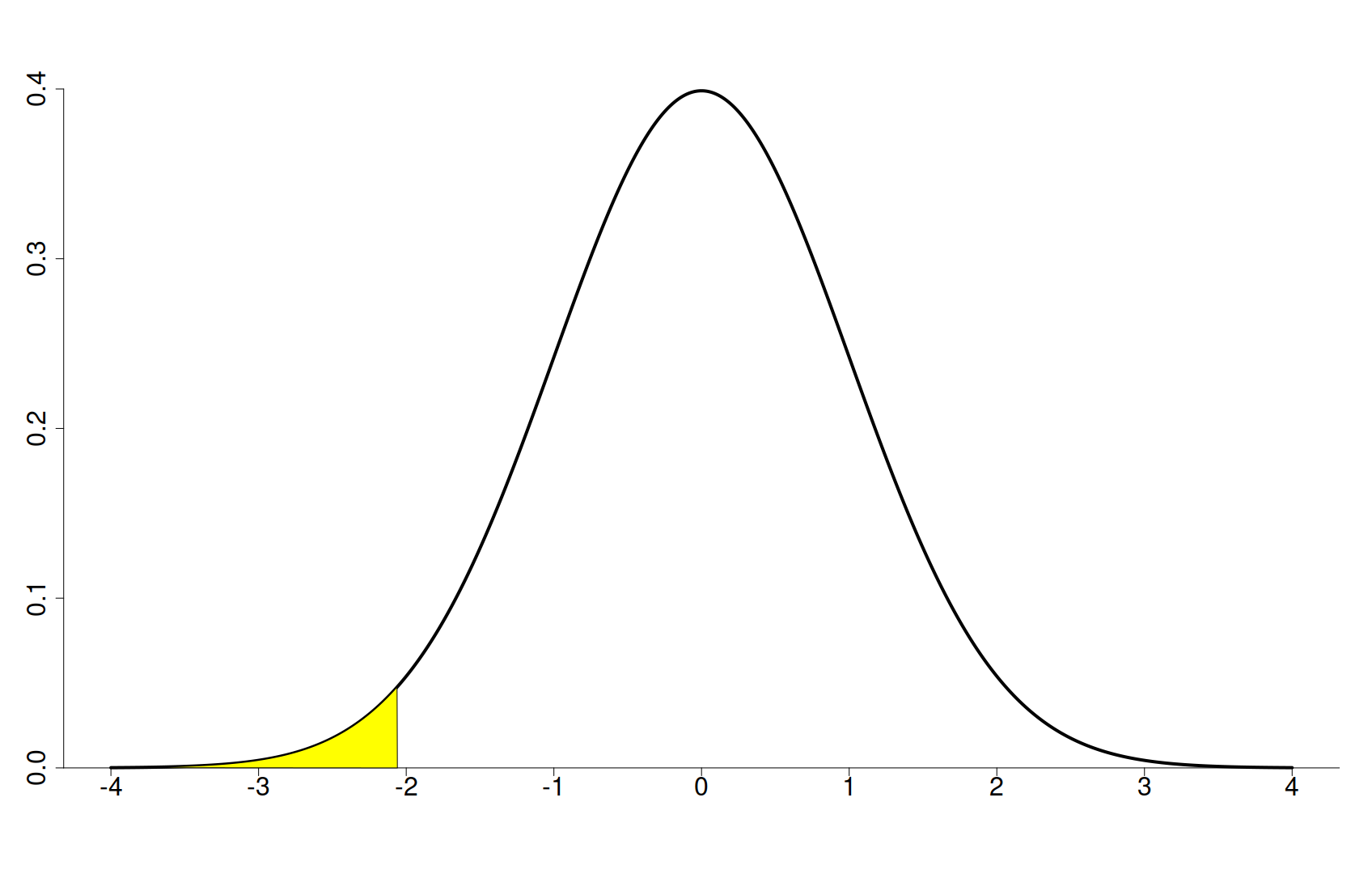
Dat fiind că distribuția de mai sus este cunoscută (distribuție normală cu medie 0 și deviație standard 1), această arie galbenă poate fi calculată cu ajutorul programelor de calcul numeric. Pentru simplitate, valorile acestei arii au fost deja calculate și se găsesc în tabele precum cele de aici.

Având în vedere că valoarea obținută de noi pentru Z este -2,068, vom privi primul tabel (cel care studiază valorile negative ale lui Z), pe linia -2,0 și coloana -0,06, citind în celula respectivă valoarea 0,01970=1,97%. Prin urmare, aria galbenă din Figura 5 este 1,97% din aria totală, ceea ce înseamnă că probabilitatea să obținem cel mult 270 cazuri de îmbolnăvire, în cazul în care vaccinul nu are efect, este de 1,97%. Acest procent poartă numele de valoare p (engleză p-value), și, de obicei, este considerat relevant când este mai mic decât 5%. Mai exact, dacă vaccinul nu ar avea efect, dat fiind că probabilitatea de a obține 270 de cazuri din 1000 este mai mică decât 5%, obținem, cu destulă siguranță din punct de vedere statistic, faptul că vaccinul are efect asupra virusului.

Un exercițiu util pentru cititorul interesat ar fi considerarea cazurilor în care avem 230 de îmbolnăviri, respectiv 290 de îmbolnăviri în rândul celor vaccinați. Întrebarea care se pune este dacă, în fiecare caz, calcularea valorilor Z și p ne permite sau nu să afirmăm cu tărie că vaccinul are efect asupra prevenirii bolii.

Concluzie

Articolul meu a încercat să introducă cititorul în universul uneori îmbârligat al statisticii matematice, scopul fiind ca, mai apoi, acesta să poată înțelege semnificația studiilor statistice pe care le citește, în particular relevanța valorii p ce apare asociată multor rezultate din aceste studii. Cunoașterea instrumentelor prezentate în acest articol constituie un bun început în demersul înțelegerii corecte a statisticilor și, în consecință, a evitării multor opinii nefondate promovate de diverse curente scientiste.

NOTE

1. Pentru a da formula de calcul a deviației standard, trebuie remarcat că, în exemplul cu înălțimea, putem calcula, pentru fiecare individ valoarea \( (h-170)^2 \), unde h este înălțimea acelui individ, iar 170 apare ca media înălțimii populației. Aceste valori \( (h-170)^2 \) sunt la rândul lor distribuite în acord cu o distribuție de probabilitate, care are, la rândul ei, o medie V (numită varianța distribuției inițiale). Deviația standard se calculează ca radicalul varianței V. ↑
2. Funcția de densitate a distribuției normale, al cărei grafic apare în figurile 1,3,4 și 6, are formula \( f(x)=\frac{1}{\sqrt{2\pi}s} e^{-\frac{(x-m)^2}{2s^2}} \), unde m este media, iar s este deviația standard. ↑
3. Dată fiind forma funcției de distribuție normală (a se vedea nota de mai sus), se poate demonstra că D e distribuită normal cu medie 0 și deviație standard \( \frac{s}{\sqrt{n}} \) dacă și numai dacă Z este distribuită normal cu medie 0 și deviație standard 1. ↑
4. Modelăm în felul următor distribuția îmbolnăvirilor: fiecare om primește valoarea X=1, dacă e bolnavă, și valoarea X=0, dacă e sănătoasă. Numărul total de îmbolnăviri este suma valorilor din eșantion. Dacă rata medie de îmbolnăvire este 30%, atunci valoarea \( (X-m)^2 \) este \( (1-3/10)^2 \) cu probabilitate 30% – când o calculăm pentru cineva bolnav – și \( (0-3/10)^2 \) cu probabilitate 70% – când o calculăm pentru cineva sănătos. Prin urmare, pentru a afla varianța, trebuie să vedem care este media acelei distribuții care ia valoarea \( (7/10)^2 \) cu probabilitate 30% și valoarea \( (3/10)^2 \) în 70% din cazuri. Media este exact \[ (7/10)^2 \cdot 3/10 + (3/10)^2 \cdot 7/10 = 21/100. \] Extragem radicalul din această valoare și obținem 0,4582. ↑

Bibliografie

Central limit theorem – Wikipedia

Hypothesis testing and p-values (video) | Khan Academy

Qualitative sense of normal distributions (video) | Khan Academy

Standard normal table – Wikipedia

(Link-urile au fost accesate în data de 11 mai 2022.)

Îi mulțumesc Alexandrei Andriciuc, doctorandă la Universitatea din București, pentru sugestille privind conținutul articolului.