Despre inteligența artificială circulă diverse opinii din ce în ce mai „inovatoare” în materie de teoria conspirației, prevăzând scenarii apocaliptice bazate pe anumite mașinării care, beneficiind de o inteligență proprie, scapă de sub controlul uman și instaurează o nouă ierarhie la nivel mondial. În final, omul ajunge să fie sclavul propriei creații, a roboților deplin autonomi. Nu știu însă câți dintre promotorii acestui tip de scenariu sunt la curent măcar cu noțiunile de bază despre rețele neurale și alte concepte matematice și informatice aflate în spatele mult vehiculatei inteligențe artificiale.
Este ușor să răspândești zvonuri despre ceva ce „sună interesant”, dar despre care nu ai habar nici la nivelul de manual pentru începători. Prin urmare, scopul acestui articol este de a prezenta, într-o manieră pe alocuri simplificată de dragul cursivității, câteva noțiuni de bază despre rețele neurale, despre cum pot acestea „învăța” și care este natura acestei învățări. Vreau să evidențiez în permanență faptul că inteligența artificială nu este decât o altă modalitate de programare, constând, la fel ca în cazul programării clasice, în algoritmi implementați de către om, acesta fiind cel ce oferă practic mașinii orice informație pe care aceasta o va deține la vreun moment sau măcar modalitatea precisă de a calcula această informație.
Bineînțeles, acest tip alternativ de programare folosește – în maniera în care istoria aviației a avut la bază observarea zborului păsărilor – observații mai mult sau mai puțin recente despre structura și funcționarea sistemului nervos al oamenilor și animalelor. Funcționarea neuronilor și interconectarea lor prin sinapse sunt ideile fundamentale ce au dus la construcția algoritmilor folosiți în acest domeniu. Totuși, suntem departe de a vorbi despre existența unor neuroni artificiali, ce au anumite capacități de gândire, ci, mai degrabă, comportamentul sistemului nervos este imitat de anumite seturi de instrucțiuni. În continuare, pornind de la simplu și trecând spre complex, voi analiza structurile matematico-informatice corespunzătoare neuronilor, sinapselor, rețelelor de neuroni și a procesului de învățare.
Deși mesajul articolului poate fi înțeles chiar făcând abstracție de formulele matematice apărute pe parcurs, am inclus, în notele de subsol, explicații intuitive pentru conceptele folosite, cu scopul de a face materialul accesibil cât mai multor cititori.
Neuroni artificiali sau doar funcții studiate în liceu?
În primul rând, anumite funcții matematice1 pot mima reacția neuronilor la anumiți stimuli primiți de la alți neuroni sau de la factori externi. Descoperirile din biologie (cf. [1], capitolul 1) arată faptul că un neuron este activat în momentul în care stimulul cumulat pe care acesta îl primește atinge un anumite prag (adică anumită intensitate minimă a stimulului). Prin urmare, avem nevoie de o funcție care să ia valoarea 0 (tradus prin neuron inactiv) pentru argumente mai mici decât un prag și valoare 1 (neuron activ) pentru argumente mai mari decât numărul ce reprezintă pragul de activare al neuronului. Graficul unei astfel de funcții este redat mai jos:
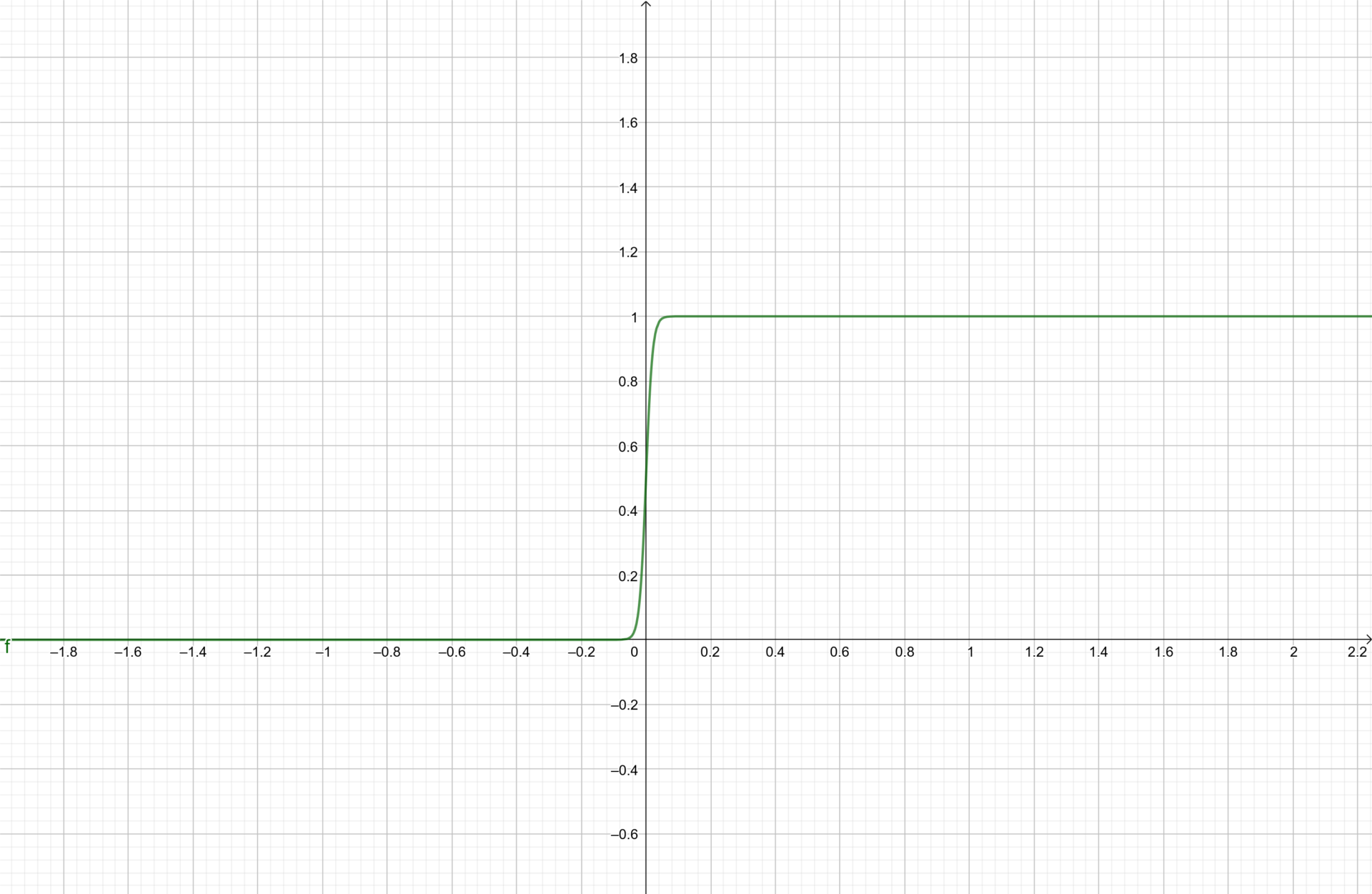
Funcția a cărei grafic2 e redat în Figura 1 este folosită în inteligența artificială cu scopul de a mima comportamentul unui neuron supus unui stimul. Ea poartă numele de funcția sigmoid și are expresia \( s(x)=\frac{1}{1+e^{-cx}} \), unde c este o constantă mai mare decât 0. Graficul din Figura 1 este trasat pentru c=100.
Observăm faptul că funcția sigmoid ia aproape valoarea 0 când argumentul x este negativ și aproape valoarea 1 când x este pozitiv. Excepție face mica regiune de tranziție din jurul argumentului 0. Astfel, pragul de care vorbeam este, în cazul funcției sigmoid, egal cu 0. Pentru a considera ca prag orice număr real \( \theta \), considerăm funcția sigmoid modificată:
\[ f_\theta(x)=s(x-\theta)=\frac{1}{1+e^{-c(x-\theta)}}, \] ce corespunde unei schimbări de stare (de la 0 la 1) în momentul în care x trece de pragul \( \theta \)3.
Acestea fiind spuse, un neuron artificial poate fi ilustrat prin următoarea schemă:
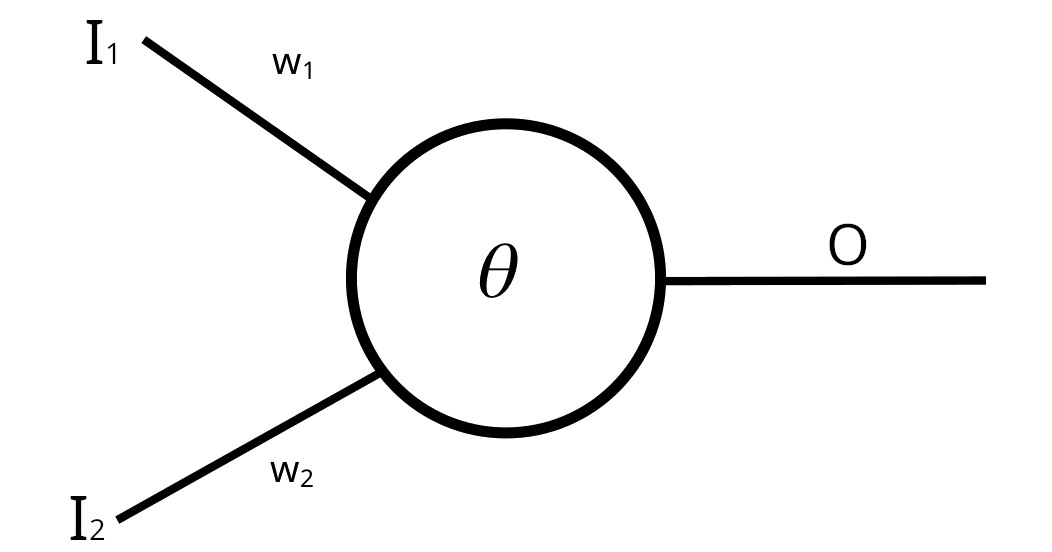
Datele de intrare I1 și I2 – provenite de la un alt neuron sau externe – sunt preluate de cele două căi din partea stângă, sunt cumulate, urmând ca funcția sigmoid să fie aplicată pentru valoarea cumulată a intrărilor, iar rezultatul O este transmis în partea dreaptă, de unde va fi preluat de un alt neuron sau afișat în exterior. Analogia biologică este clară: intrările reprezintă dendritele neuronului, iar în partea dreaptă avem echivalentul axonului. Totodată, în funcționarea unui neuron uman, unele căi de intrare sunt mai semnificative (i.e. contează mai mult) decât altele. Această distincție cantitativă este cuantificată prin niște numere (în figură, w1 și w2), numite ponderi, asociate fiecărei intrări.
Pentru a ilustra funcționarea acestui tip de legături ponderate, presupunem că neuronul primește stimulul cu valoarea (i.e. intensitatea) 2 prin intrarea de sus și stimulul cu valoarea 3 pe intrarea de jos. Datorită ponderilor w1 și w2 ale celor două intrări, valoarea cumulată pe care neuronul o receptează este \( 2\cdot w_1 +3\cdot w_2 \)4, semnalul primit prin legătura cu pondere mai mare participând mai mult la valoarea efectivă de intrare. Astfel, rezultatul pe care neuronul îl furnizează mai departe tuturor neuronilor de pe nivelul următor este \( s_{\theta}(2\cdot w_1 +3\cdot w_2 -\theta) \) (adică activitatea/gândirea pe care o exercită neuronul este calcularea rezultatului unei funcții – sigmoid modificată – având ca argument data de intrare). Valoarea astfel obținută este transmisă mai departe altor neuroni și va fi receptată mai intens sau mai slab în funcție, din nou, de ponderile legăturilor către acei neuroni.
Rețele neurale sau doar compuneri de funcții?
În continuare, vom studia interconectarea neuronilor artificiali, formând așa-numitele rețelele neurale, echivalentul informatic al sinapselor din sistemul nervos.
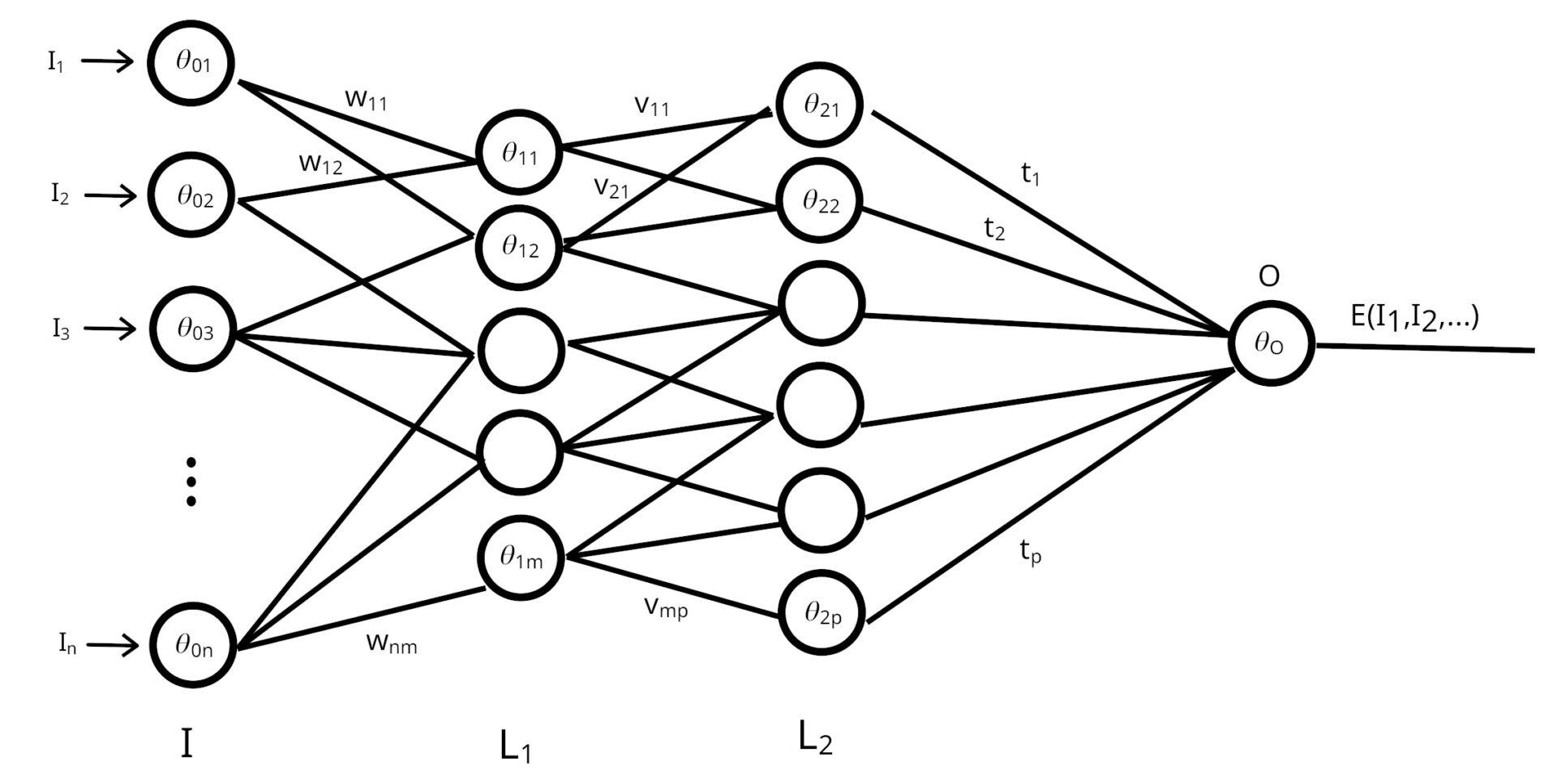
În structura din Figura 3, neuronii artificiali sunt grupați pe mai multe niveluri, nivelul inițial „I” fiind cel în care datele intră în sistem. Restul nivelurilor L1, L2 etc. fiind nivelurile interne ale rețelei (neuronii de aici nu primesc și nu transmit informații din/către exterior). Fiecare neuron de pe un nivel este conectat cu toți neuronii de pe nivelul următor, iar conexiunile au asociate câte o valoare (numită pondere), notată pe frigură prin w11, w12, v11, v21, t1, t2 etc5. Cu cât aceasta este mai mare, cu atât conexiunea respectivă este mai semnificativă. Spre exemplu, neuronul din stânga sus (ce are notat pe el pragul \( \theta_{01} \) ) primește din exterior stimulul I1, pe care îl transmite mai departe tuturor neuronilor de pe nivelul L1. Apoi, neuronul \( \theta_{11} \) interceptează stimuli de la toți neuronii de pe nivelul „I”, mai intens sau mai slab în funcție de ponderile w11, w12 etc. Rezultatul pe care acest neuron îl furnizează va fi apoi transmis către toți neuronii de pe nivelul L2, procesul continuând până se obține rezultatul final la nivelul neuronului notat cu „O”.
Deși sună foarte sofisticat să vorbim despre rețele de neuroni artificiali, explicația de mai sus arată că acestea nu sunt decât niște compuneri de funcții6. Având în vedere că prin neuroni artificiali înțelegem funcția sigmoid aplicată sumei ponderate a unor date de intrare, trecerea de la un nivel al rețelei la următorul reprezintă aplicarea acestei funcții (sigmoid cu pragul neuronului receptor) rezultatului altei funcții (corespunzătoare neuronului emițător), adică, așa cum spuneam, o compunere de funcții.
Astfel, rezultatul final de ieșire din rețea pe care neuronul „O” îl furnizează reprezintă o funcție (obținută prin sumări ponderate succesive și aplicarea funcției sigmoid) ce are ca argumente datele de intrare I1, I2,…, In, ponderile (w11, v12 etc.) și pragurile \( \theta_{01} \), \( \theta_{02} \), ,\( \theta_{12} \) etc. ale tuturor neuronilor. Putem scrie cumulat întreaga rețea ca o funcție:
\[ E(I_1,I_2,\ldots I_n,w_{11},w_{12},w_{21},\ldots,v_{11},v_{12},v_{21},\ldots,t_1,t_2,\ldots, \theta_{01},\theta_{02}\ldots) \]
Bineînțeles, rețelele neurale pot avea mai multe căi de ieșire, dar, pentru simplificarea expunerii, ne-am limitat la o rețea care furnizează o singură valoare ca dată de ieșire.
Mașini gânditoare sau doar minimul unei funcții?
Trecem acum la întrebarea cea mai răspândită când vine vorba despre inteligența artificială: cum poate un computer să învețe și să „gândească”. Răspunsul e: imitând învățarea umană în sensul în care algoritmul este conceput să minimizeze erorile pe care le face. Astfel, în etapa de învățare, algoritmul primește multe seturi de date de intrare, pentru fiecare primind și rezultatul final ce ar trebui obținut.
Eroarea pentru fiecare set este dată de diferența dintre valoarea obținută aplicând funcția E datelor de intrare și valoarea scontată (eroarea este dată de această diferență ridicată la pătrat, din rațiuni practice). Pentru a vedea cum poate fi minimizată eroarea, trebuie avut în vedere ce parametri ai rețelei se pot ajusta.
La o privire atentă, în scrierea funcției E – ce corespunde întregii rețele – intervin două tipuri de argumente. Unele sunt clar definite ca date externe de intrare (I1, I2,…, In) – furnizate de programator sau utilizatori – și restul (ponderile și pragurile) sunt proprii rețelei și pot fi modificate pentru a optimiza rezultatul, adică a minimiza eroarea. Astfel, trebuie găsite valorile ponderilor și pragurilor pentru care suma erorilor aferente tuturor seturilor de date de intrare și valoare scontată este minimă. Dar această eroare nu este decât o nouă funcție ce ia ca argument ponderile și pragurile (căci seturile de date de învățare sunt prestabilite)7.
Pentru a fi mai clari, să presupunem că, în procesul de învățare, rețeaua primește două seturi fixate anterior de date de intrare și valoare scontată notate prin (I11, I12,…, I1n ;S1) și (I21, I22,…, I2n ;S2). Atunci eroarea totală este:
\[Err = (E_1-S_1)^2+(E_2-S_2)^2, \]
unde E1 este rezultatul aplicării funcției E pentru primul set de date și E2 pentru al doilea set, iar S1 și S2 sunt valorile scontate. Deoarece seturile de date sunt fixate (furnizate de programator sau un utilizator al programului), funcția Err va depinde doar de ponderi și praguri8. Cu cât valoarea funcției Err este mai mică, cu atât rețeaua operează mai bine pe seturile primite în procesul de învățare9. În concluzie, algoritmul de învățare trebuie să includă o metodă de a găsi ponderile și pragurile optime pentru a minimiza funcția eroare. Toată problema este redusă la a găsi un minim pentru o funcție cu mai multe variabile.
În această secțiune voi descrie succint și strict intuitiv una dintre metodele de minimizare folosite în antrenarea rețelelor neurale. Metoda poartă numele de „Coborâre în gradient” [engl. Gradient Descent] și poate fi ilustrată prin următoarea imagine, în care suprafața albastră reprezintă graficul unei funcții – notate pentru coerență tot Err(w1,w2) – de două variabile10.

Dorim să găsim valorile optime (w1,w2) pentru care funcția să ia valori minime (adică înălțimea punctului de pe grafic aflat deasupra poziției (w1,w2) de pe podea să fie minimă). Pe scurt, ne interesează să găsim poziția punctului F aflat cel mai jos pe suprafață. Algoritmul de minimizare poate fi descris intuitiv după cum urmează: vrem să găsim fundul F al vasului din Figura 4. Avem la îndemână o bilă, pe care o așezăm oriunde pe suprafața interioară a vasului și o lăsăm liberă. Ea va urma direcția cea mai abruptă de coborâre spre fundul castronului.
Formalizând matematic, începem cu valori arbitrare ale lui w1 și w2 (în practică, ponderile inițiale ale rețelei neurale vor fi alese arbitrar) și considerăm punctul corespunzător A de pe grafic. În acel punct, găsim direcția cea mai abruptă în jos (pe figură, săgeata galbenă la A la B), proces ce implică un calcul de derivate. Pentru cititorul care are cunoștințe superioare de matematică, această direcție este \( -\nabla Err(w_1,w_2) \), adică opusul gradientului funcției în punctul (w1,w2).
Prin urmare, tot procesul de învățare artificială nu este decât o (foarte ingenioasă) aplicare a derivatei compunerii unor funcții, urmată de ajustarea argumentelor. Esența este aceeași ca în găsirea punctelor de minim pentru funcții, familiară elevilor de clasa a XI-a de la profilul real.
Un exemplu de problemă rezolvată cu ajutorul rețelelor neurale
În această secțiune finală, voi încerca ilustrez întreg procedeul de mai sus în cazul unei probleme concrete, evidențiind totodată importanța acestui tip de algoritmi care pot „învăța” din exemple. Considerăm următoarele două imagini:

Pentru un om, nu există nicio îndoială că în prima imagine apare cifra 3, iar în a doua cifra 5. Totuși, ar fi extrem de dificil pentru cineva să descrie (și, mai mult, să implementeze pe calculator) un algoritm precis care furnizează cifra respectivă, având ca date de intrare culorile celor 81 de pătrate din chenar. În aceste cazuri, rețelele neurale ca cele din Figura 3 sunt soluția salvatoare. Considerând o astfel de rețea cu datele de intrare I1, I2…, I81 reprezentând culorile celor 81 de pătrate (ne interesează doar tonuri de gri, așa că putem codifica 0=alb, 1=negru și orice valoare între 0 și 1 pentru tonuri de gri). Rezultatul final O va fi rotunjit la cea mai apropiată cifră 0,1,…, 9 pentru a obține cifra recunoscută de sistem.
Tot ce rămâne de făcut este să „antrenăm” rețeaua, adică să aplicăm algoritmul de minimizare a erorii pentru un set imens de date de intrare. Adică numeroase seturi de imagini ca în Figura 5, împreună cu cifra scontată (în exemplu dat, cifra 3, respectiv 5) vor fi furnizate de programator sau utilizatori. După acest proces de adaptare a ponderilor și pragurilor, rețeaua va fi calibrată pentru a recunoaște și alte imagini în afara celor primite în procesul de învățare. Totul se bazează pe similaritatea acestor noi imagini cu anumite exemple primite de algoritm în timpul „antrenamentului”, exemple care au dus la ajustarea parametrilor pentru minimizarea erorii. Similaritatea dintre imaginea nouă și exemple face ca, în cazul unei imagini noi, eroarea dintre rezultatul oferit de rețea și cel corect să fie, de asemenea, mică.
Concluzie: Mașini inteligente sau doar algoritmi creați inteligent?
Având în minte explicațiile din acest articol, putem identifica cu ușurință cauza care generează impresia că o mașinărie ar gândi, și anume faptul că programatorul creează doar cadrul (structura rețelei), dar nu definește el însuși ponderile, ci doar implementează algoritmul prin care aceste ponderi (și praguri \( \theta \)) optime sunt găsite. Totuși, dacă ne referim la setul de date de învățare ca făcând parte integrantă din program, atunci procesul de obținere a parametrilor optimi este complet determinist, similar unui program clasic. Prin urmare, nu calculatorul care „gândește” este problema, ci persoanele care stau în spatele acestuia, îl programează și îl antrenează. Zicala „Cum ți-i crești, așa îi ai” referitoare la copii este cât se poate de aplicabilă în problematica inteligenței mașinilor.
NOTE
- Pentru cititorul nefamiliar cu noțiunea de funcție, voi încerca să fac o prezentare cât mai clară și intuitivă. Numim funcții anumite obiecte matematice, capabile să calculeze un anumit rezultat pornind de la date datele de intrare pe care aceasta le primește. Spre exemplu, funcția „culoarea ochilor” ia ca dată de intrare o persoană și oferă ca rezultat o culoare. Faptul că aplicăm funcția unei anumite date de intrare (numită în continuare argument al funcției – fără legătură cu înțelesul curent al termenului argument) se exprimă prin notația nume_funcție(argument). În exemplul de mai sus, avem verde=culoare_ochi(Mihai). culoare_ochi este numele funcției, Mihai este argumentul funcției, iar verde este rezultatul sau valoarea funcției calculate în argumentul Mihai. Funcțiile pot avea mai multe argumente. Spre exemplu, funcția adunare are două argumente, iar rezultatul ei este suma argumentelor, 5=adunare(2,3). ↑
- Graficul unei funcții este o reprezentare în plan (sau în spațiu, cum vom vedea la sfârșitul articolului) a valorii pe care funcția o ia când argumentul este unul numeric. În graficul din Figura 1, înălțimea la care se află linia îngroșată deasupra unui punct de pe axa orizontală reprezintă valoarea funcției sigmoid, când argumentul este acel punct (i.e. numărul asociat acestui punct). ↑
- Adică această nouă funcție ia aproape valoarea 0 pentru argumente mai mici decât θ și aproape valoarea 1 pentru argumente mai mari decât θ, cu excepția unei mici porțiuni de tranziție în jurul pragului θ. ↑
- Spre exemplu, dacă w1=1 și w2=2, atunci neuronul va primi ca dată de intrare \( 2\cdot 1 + 3\cdot 2 =8 \); practic, valoarea primită pe canalul de jos contează de două ori mai mult la valoarea primită în final, deoarece are pondere (w2=2) dublă față de canalul de sus (care are ponderea w1=1). ↑
- Indicii ponderilor și pragurilor θ01, θ02 etc. au doar rolul de a ne face atenți că aceste ponderi și praguri sunt diferite pentru fiecare neuron în parte. ↑
- Compunerea de funcții se referă la aplicarea unei funcții având ca argument valoarea altei funcții. Spre exemplu, compunerea dintre funcția număr de litere și culoarea ochilor este ilustrată prin număr_litere( culoare_ochi( Mihai )) = 8, căci culoare_ochi(Mihai)=albastru, cuvânt format din 8 litere. Un exemplu numeric poate fi dublu(adunare(3,4))=dublu(7)=14. ↑
- Este ca și cum am defini funcția adunare_cu_doi, pornind de la funcția adunare, căreia îi fixăm primul argument: adunare_cu_doi(x)=adunare(2,x)=2+x. Prin urmare, obținem o funcție cu mai puține argumente. La fel și în cazul funcției E, fixând argumentele I1, I2 etc., obținem o funcție ce depinde doar de ponderi și praguri. ↑
- A se vedea nota de subsol nr. 7. ↑
- Suma a două numere pozitive este cu atât mai mică, cu cât fiecare dintre aceste numere este mai mic. Astfel, Err este cu atât mai mică cu cât E1 este mai aproape de S1 (i.e. diferența lor este mai mică) și E2 este mai aproape de S2. ↑
- Principiul de reprezentare este același ca în cazul graficului din Figura 1. Înălțimea la care se află punctul A reprezintă valoarea Err(x,y) a funcției în perechea (x,y) determinată de umbra lui A pe „podeaua” 2-dimensională. ↑
BIBLIOGRAFIE
[1] Rojas, R., Neural Networks – A Systematic Introduction, Springer-Verlag, Berlin, New-York (1996).↑
[2] Seria de videoclipuri „Rețele Neurale” a canalului de YouTube 3Blue1Brown (accesat 18 ianuarie 2022).
[3] Pentru explicații suplimentare despre metoda Coborârii în gradient, puteți consulta videoclipul Gradient Descent, Step-by-Step (accesat 18 ianuarie 2022).
Imagine: Pixabay

Întotdeauna am considerat termenul „Inteligență artificială” ca fiind doar o chestiune de marketing. Eu îi spun tot „machine learning”; mașina învață de la cineva sau ceva, deci sunt de acord cu concluzia din articol.