Syntopic

Acest articol este o continuare a articolului Câteva intuiții matematice pentru noțiuni teologice (partea I) și are, la fel ca acela, scopul de a arăta că oamenii de știință preocupați de matematică lucrează cu idei la fel de puțin intuitive ca cele din teologia ortodoxă, iar unele dintre aceste noțiuni matematice pot da o intuiție (parțială, bineînțeles) pentru cele teologice.

Cititorilor care nu sunt familiarizați cu noțiunea de numere cardinale le recomand citirea articolului precedent.

A treia intuiție teologică

Această intuiție se bazează pe faptul că o linie dreaptă (nemărginită) și un segment de dreaptă au același număr de elemente, chiar dacă cel de-al doilea este mărginit.

Pentru a demonstra acest fapt, considerăm dreapta ca fiind axa numerelor reale (orizontală) în plan, iar segmentul fiind porțiunea cuprinsă între numerele -1 și 1 (din motive tehnice, alegem ca segmentul să nu conțină capetele -1 și 1, ci doar punctele din interior).

În primul rând, vom construi asocierea bijectivă între segmentul (-1,1) și un cerc, din care scoatem un punct. Deși această asociere se poate scrie riguros, prefer să o descriu vizual prin următoarea animație:

Punctele A și B sunt suprapuse peste punctul cel mai de sus al cercului, „polul nord”. Punctele din interiorul intervalului sunt asociate bijectiv cu punctele de pe cercul din care scoatem „polului nord”. Rezultă că segmentul (-1,1) are tot atâtea elemente cât un cerc din care lipsește un punct.

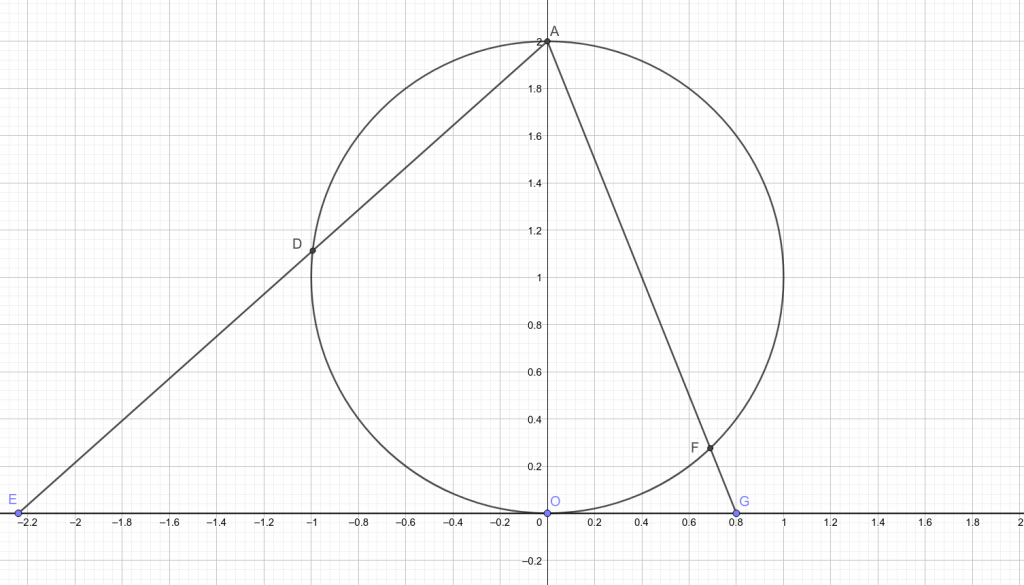
Pentru fiecare punct D de pe cerc (fără “polul nord”, notat A), considerăm dreapta AD. Aceasta intersectează dreapta reală într-un unic punct (pe figură E). Aceeași corespondență e descrisă și de perechea F-G. Am construit astfel o asociere bijectivă intre dreaptă și cercul fără un punct. Prin urmare, cele două mulțimi au același număr de elemente. (Remarcăm faptul că scoaterea polului nord din prima mulțime este doar o chestiune tehnică, menită să faciliteze construcția corespondenței bijective, întrucât dreapta orizontală prin punctul A nu intersectează axa reală. Asocierea dată se poate modifica, astfel încât întreg cercul să fie pus în corespondență cu dreapta.)

Punând totul cap la cap, am obținut că segmentul (-1,1) are la tot atâtea elemente cât un cerc din care s-a scos un punct, iar acesta cât întreaga dreaptă. Deci segmentul este la fel de mare (în sensul numărului de elemente) ca și dreapta. Inversând construcția de mai sus, putem transforma un obiect nemărginit (dreapta) într-un obiect mărginit (segmentul), fără a-i altera mărimea.

Având în minte această construcție, unui matematician nu i se va părea ciudat să audă despre Întruparea Fiului lui Dumnezeu următoarele texte de slujbă:

Dumnezeul cel mai presus de ființă și Domnul, din tine Preacurată, S-a întrupat pentru bunătate, înființându-Se ca noi și rămânând ceea ce a fost. (Canonul Sfintei Treimi din Octoihul Mare, glas 3)

Trasu-ne-ai pe noi spre dragostea Ta, mult-milostive Cuvântule al lui Dumnezeu, Carele pentru noi Te-ai întrupat fără de schimbare (…) (Canonul Sfintei Treimi din Octoihul Mare, glas 3)

Minune prea mare, cum Cel neîncăput S-a ţinut în pântecele tău şi S-a întrupat şi S-a arătat ca un om, nesuferind amestecare, sau despărțire de dumnezeiasca şi neschimbata Dumnezeire (…) (Canonul Sfintei Treimi din Octoihul Mare, glas 3)

De mărirea părintească nedepărtându-Te, la a noastră prostime Te-ai pogorât de voie, întrupându-Te, Cel ce eşti mai presus de fiinţă, și pe toți i-ai înălțat la dumnezeiasca mărire, ca un milostiv. (Canonul Sfintei Treimi din Octoihul Mare, glas 7)

(…) Că ispită de bărbat neluând, ceea ce ești cu totul fără prihană, ai născut fără de tată pe Fiul cu trup, pe Cel născut din Tatăl mai-nainte de veci fără mamă, Carele nicicum n-a răbdat schimbare, sau amestecare, sau despărțire, ci a păzit întreagă deosebirea amândurora firilor. (Dogmatica, Vecernia de sâmbătă seară, glas 3)

Cela ce a zidit pe Adam, Se poartă ca un Prunc. Cel neîncăput, încape în brațele bătrânului. Cel ce este în Sânurile cele necuprinse ale Părintelui său, de bunăvoie se cuprinde cu trupul, iar nu cu Dumnezeirea (…) (Icosul Întâmpinării Domnului)

A patra intuiție teologică

Pentru cea de-a patra intuiție, voi pleca de la două citate teologice:

Căci vedem acum ca prin oglindă, în ghicitură, iar atunci, față către față; acum cunosc în parte, dar atunci voi cunoaște pe deplin. (1 Corinteni, XXXIII, 12)

Și acum în ceruri, oglinzile dezlegându-se Fericite, curat vezi Sfânta Treime, rugându-te fără mijlocire, pentru cei ce cu credință şi cu dragoste te cinstesc pe tine. (Slujba Sfântului Antonie cel Mare)

Deși nu pot ști exact ce fel de intuiție vizuală au avut autorii textelor de mai sus, cu privire la sintagma „ca prin oglindă”, voi încerca să arăt cum s-ar putea înțelege parțial aceasta prin ochii unui matematician. Voi vorbi despre coordonate în spațiu și despre spații cu mai mult de trei dimensiuni.

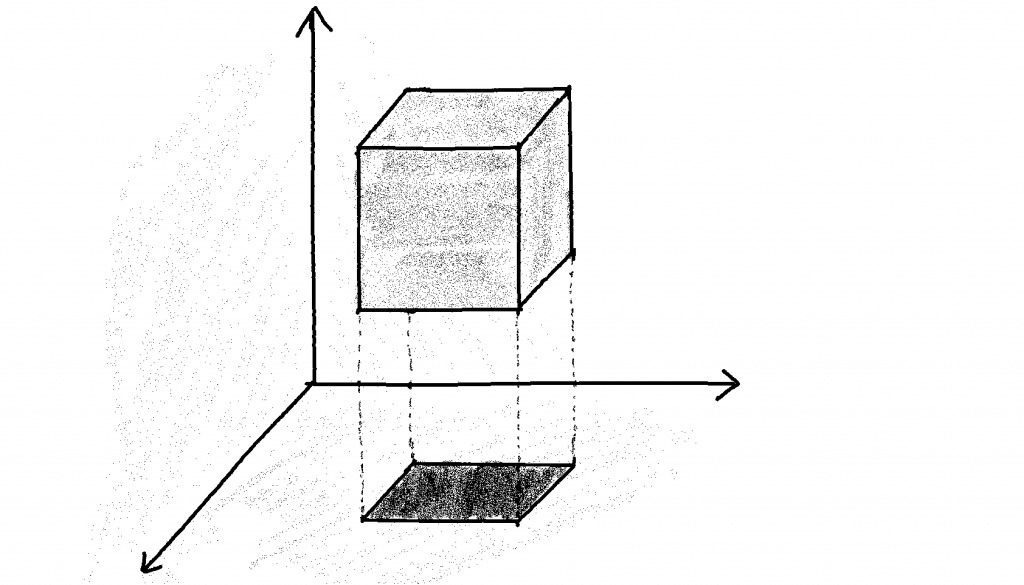
În primul rând, ne imaginăm o încăpere, reprezentată în figura de mai sus. La intersecția celor trei linii este un colț al camerei. Afirm că fiecare punct din interiorul camerei poate fi descris prin exact trei numere. Spre exemplu, punctul corespunzător numerelor (3; 2,5; 1) se găsește plecând din colțul evidențiat, mergând trei metri în dreapta, apoi doi metri și jumătate în față și un metru în sus. Similar, având orice triplet de numere (x; y; z), găsim un unic punct din interiorul camerei. Cu aceste notații, podeaua poate fi descrisă drept mulțimea punctelor la care nu e necesară urcarea, adică al treilea număr din triplet este egal cu 0. Punctele de pe podea sunt descrise exact de doar două numere, primul arătând deplasarea în dreapta, iar al doilea deplasarea în față.

Folosind convențiile de mai sus, putem defini ce înseamnă proiecția unui obiect tridimensional pe planul podelei. Ca în figura de mai sus, considerăm un cub plutind în cameră și umbra sa pe podea (sursa de lumină este aflată pe întregul tavan). Umbra punctului (x; y; z) al cubului este exact punctul (x; y; 0) de pe podea. Deci umbra (matematic spus, proiecția) cubului pe planul podelei este formată din toate punctele de forma (x; y; 0), pentru care există un număr z astfel încât (x; y; z) este punct al cubului. Remarcăm faptul că doar din proiecția unui obiect nu putem deduce întreaga formă a acestuia. Spre exemplu, obiectul poate fi oricât de înalt și, totuși, să genereze aceeași proiecție. Aproximativ același lucru se întâmplă și cu o oglindă. Pe suprafața plană a oglinzii se proiectează obiectele din cameră, acestea reducându-se practic la două dimensiuni.

Următorul pas este un exercițiu de imaginație. Să ne imaginăm o creatură ce are doar două dimensiuni. Trăiește în planul podelei din figura de mai jos (să zicem în punctul A) și poate vedea (percepe) doar obiecte din planul podelei.

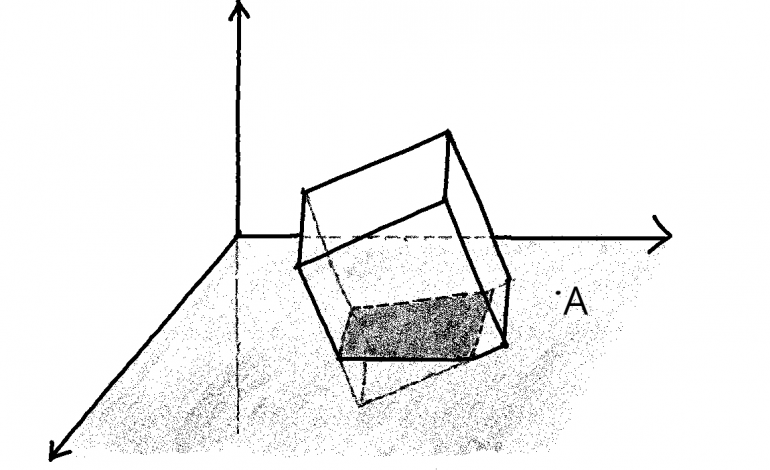
În cazul unui cub din spațiu, oare ce poate percepe creatura noastră? Pentru a da răspunsul, vom introduce cubul în planul podelei (în acest moment, ar fi bine să ne imaginăm podeaua ca fiind suprafața unui lichid, spre exemplu o piscină cu apă). Din toată forma cubului, creatura percepe doar patrulaterul hașurat în desen, dat de intersecția cubului cu suprafața apei. Ea nu poate nici măcar concepe cum arată un cub tridimensional.

Pentru obiecte aflate deasupra podelei, creatura poate distinge doar informații referitoare la proiecția acestora pe podea. Pentru ea, cubul din prima figură nu este altceva decât un pătrat.

Intuiția pentru cele două citate mai necesită încă un exercițiu de gândire, de data aceasta în patru dimensiuni. Aici, coordonatele (numerele) introduse la început vor juca un rol important, deoarece formalismul descris de ele ne permite sa „vedem” punctele unui spațiu cu patru dimensiuni ca fiind cvadruplete de puncte (x; y; z; t). Spațiul tridimensional obișnuit joacă rolul „podelei” în acel spațiu, ale cărei puncte (x; y; z; 0) sunt descrise de exact trei numere. Ne este foarte greu, dacă nu imposibil, să intuim cum arată obiectele din acest spațiu cu patru dimensiuni, la fel cum creaturii bidimensionale îi era imposibil să perceapă cubul în întreaga lui formă.

Precum aceasta vedea proiecția cubului, și noi putem vedea („ca prin oglindă”) proiecții ale obiectelor patru-dimensionale, dar numai „în ghicitură”, nefiind capabili să sesizăm toate aspectele unui corp cu patru dimensiuni. Dacă acea creatură ar fi ridicată din plan și înzestrată cu vederea în trei dimensiuni, atunci cubul i-ar apărea cum este el în realitate. Iar noi, depășind constrângerile lumii tridimensionale, am percepe plenitudinea obiectelor cu mai mult de trei dimensiuni, „oglinzile dezlegându-se”.

Imagine: Unsplash