Actualul manual de logică pentru clasa a IX-a, aflat în vigoare deja de aproape 17 ani, nu a fost, până acum, obiectul unei discuții critice, sistematice. De ce este important?
Din două motive principale: în primul rând, manualul are multe neajunsuri importante, atât științifice, cât și didactice – sau, aceasta este ceea îmi propun să arăt mai departe, pe parcursul lucrării. De aceea, o discuție critică este mai mult decât necesară.
În al doilea rând, ne aflăm într-un moment în care sunt propuse noi planuri-cadru pentru învățământul liceal. O discuție serioasă privitoare la statutul logicii este, cred, una dintre cele mai urgente chestiuni ce trebuie rezolvate.
Întâi, câteva informații generale:
- Elena Lupșa, Victor Bratu, Maria Dorina Stoica, Logică și argumentare. Manual pentru clasa a IX-a, Editura Corvin, Deva, 2004 (Lupșa, Bratu, & Stoica, 2004).
- Manualul a fost aprobat prin ordinul de ministru 3886/2004.
- Programa analitică aflată în vigoare în acest moment (anul școlar 2021 – 2022) a fost aprobată prin ordinul de ministru 5099/2009. Manualul a fost realizat în conformitate cu programa analitică aprobată prin ordinul de ministru 3458/2004.
Ce îmi propun? Să scot în evidență câteva dintre neajunsurile științifice și didactice pe care le are acest manual de logică.1 Astfel, în prima secțiune a lucrării voi avea în vedere conținutul manualului, din punct de vedere științific; în a doua secțiune voi spune câte ceva despre virtuțile didactice ale acestuia.
Trebuie spus din capul locului că nu intenționez discutarea exhaustivă a manualului, ci să scot în evidență acele aspecte pe care le consider suficiente pentru buna întemeiere a concluziilor pe care le voi formula. Astfel, în prima secțiune – științifică – mă voi concentra asupra a două astfel de aspecte: caracterizarea conceptului de validitate și tratarea inferențelor imediate cu propoziții categorice; în a doua secțiune, voi formula câteva observații de natură didactică.
Știința logicii
Validitatea inferențelor
Încep discuția luând în considerare conceptul de validitate a unei inferențe. Motivul este simplu: validitatea este conceptul central al logicii. Capacitatea de a oferi instrumente riguroase ce permit discernerea inferențelor valide de cele nevalide este pretenția teoretică fundamentală a cercetării logice. Prin urmare, tratarea corectă a conceptului de validitate este esențială pentru orice lucrare de logică – fie ea de cercetare sau didactică.
În manualul de logică, definiția validității inferențelor poate fi găsită la pagina 36. După ce operează distincția dintre inferențele deductive și cele nedeductive, autorii scriu:
„O inferență deductivă este validă atunci când din premise adevărate se obține concluzie adevărată.” (sublinierile în original – nota mea)
Definiția oferită este problematică în mai multe privințe. În primul rând, se poate observa aproape imediat că definiția nu este caracteristică, deoarece definitul și definitorul se află în raport de încrucișare: cu alte cuvinte, există inferențe nevalide cu premisele și concluzia adevărate, după cum există inferențe valide ce nu au premisele și concluzia adevărate.
În al doilea rând, un comentariu privitor la forma definiției. Se poate observa că aceasta poate fi reformulată astfel: dacă premisele și concluzia unei inferențe [deductive]2 sunt adevărate, atunci inferența este validă.
Cu alte cuvinte, adevărul premiselor și concluziei este un temei (doar) suficient pentru ca inferența să fie validă. Or, nu de la așa ceva ne așteptam în formularea unei definiții, ci de la formularea unei identități între termenul definit și termenii definitori. Cu alte cuvinte, din perspectiva formei logice, definiția ar trebui formulată ca o propoziție bicondițională de forma: O inferență este validă dacă și numai dacă…
În sfârșit, ne putem întreba cu privire la sensul verbului „se obține”: dacă înseamnă, pur și simplu, „este derivată”, atunci definiția este greșită în sensul de mai sus; dacă îi adăugăm un calificativ de felul „riguros, corect etc.”, atunci definiția devine suspectă de circularitate: o inferență deductivă este validă atunci când din premise adevărate se obține corect, riguros (valid?) o concluzie adevărată. Cu alte cuvinte, definitorul pare să conțină termenul definit.
Imediat după ce definesc validitatea unei inferențe [deductive], autorii manualului oferă și definiția nevalidității unei inferențe [deductive]:
„O inferență deductivă este nevalidă atunci când premisele pot fi adevărate, însă concluzia este falsă.” (sublinierile în original – nota mea)
Desigur, observația de mai sus referitoare la forma definiției se aplică și aici. Nu o reiau.
Definiția este, însă, interesantă și relevantă pentru discuția noastră, deoarece este în direcția corectă (deși, ar fi putut fi exprimată ceva mai simplu) și oferă indiciile pentru o definire corectă a validității însăși.
Într-adevăr, definiția nevalidității conține expresia-cheie „pot fi”, iar aceasta este direcția corectă. Motivul este, desigur, acela că validitatea unei inferențe privește relația dintre valoarea de adevăr a premiselor și cea a concluziei. Astfel, o inferență este validă dacă și numai dacă în orice situație în care premisele sunt adevărate, concluzia va fi adevărată. Cu alte cuvinte, nu este posibil ca premisele să fie adevărate și concluzia falsă3. Decurge mai departe că inferența este nevalidă dacă și numai dacă este posibil ca premisele să fie adevărate și concluzia falsă – ceea ce este exact definiția de mai sus, cea din manual.
Nu este cazul să insist. Definirea validității nu este cea mai mare problemă științifică a manualului, iar evidențierea ei nu este necesară pentru stabilirea concluziei principale a lucrării.
Inferențe imediate cu propoziții categorice
Lăsând, așadar, la o parte discuția despre conceptul general de validitate, voi continua luând în considerare o altă secțiune importantă a manualului, anume propozițiile categorice și inferențele imediate cu propoziții categorice (incluzând aici și raporturile de opoziție). Pentru ca lucrarea să nu devină inutil de lungă, nu voi avea în vedere și capitolul despre silogism, deși voi face câteva mențiuni și în acest sens. Concluziile pe care le voi întemeia sunt următoarele:
- Deși inferențele imediate (inclusiv raporturile de opoziție) sunt prezentate în modul obișnuit, supozițiile existențiale atribuite propozițiilor categorice nu validează aceste inferențe.
- Mai mult, mulțimile de inferențe imediate validate sunt diferite și incompatibile. Vom vedea, de exemplu, că raportul de contradicție este valid într-o anumită interpretare a propozițiilor și nevalid în altă interpretare, iar aceste interpretări diferite sunt prezentate ca și cum ar fi echivalente; aceeași problemă apare și în legătură cu alte inferențe imediate, precum conversiunea sau inversiunea. Existența unor astfel de situații, alături de situația prezentată de prima concluzie, oferă bune temeiuri pentru acuzația de inconsistență la adresa aparatului logic prezentat în manual.
Voi proceda astfel:
- Voi defini conceptul – central în această discuție – de supoziție existențială a unei propoziții categorice și voi formula problema supoziției existențiale pentru propozițiile categorice;
- Voi reprezenta formele logice ale propozițiilor categorice atât cu supoziție existențială, cât și fără4.
- Voi întemeia, pe baza formalizărilor făcute, acuzația de incoerență sau inconsistență la adresa manualului.
Întâi, câteva prescurtări:
A = df Toți S sunt P. (SaP)5
E = df Niciun S nu este P. (SeP)6
I = df Unii S sunt P. (SiP)7
O =df Unii S nu sunt P. (SoP)8
Definiție: o propoziție categorică are supoziție existențială dacă și numai dacă nu poate fi adevărată decât dacă subiectul său logic este un termen nevid (i.e., denotă cel puțin un obiect existent în universul de discurs). De exemplu, propoziția particular-afirmativă „Unele insecte sunt prădători de temut” poate fi adevărată numai dacă subiectul său logic – termenul „insecte” – se aplică unor ființe reale: insectele.
Problema supoziției existențiale este următoarea: cum trebuie înțelese propozițiile categorice în ceea ce privește supoziția existențială? Ce inferențe pot fi considerate valide în funcție de supozițiile existențiale atribuite propozițiilor categorice?
Din fericire, chestiunea poate fi tratată într-o manieră generală, exploratorie, fără a fi nevoiți să luăm o decizie referitoare la modul cel mai adecvat în care trebuie înțelese propozițiile categorice. Astfel, pentru fiecare propoziție categorică există două situații posibile ce trebuie considerate: are supoziție existențială sau nu are9. Vom avea, prin urmare, opt situații posibile, astfel:
- A∃: Există S și toți S sunt P.
- A~∃: Nu există S sau toți S sunt P.
- E∃: Există S și niciun S nu este P.
- E~∃: Nu există S sau niciun S nu este P.
- I∃: Există S și unii S sunt P.
- I~∃: Nu există S sau unii S sunt P.
- O∃: Există S și unii S nu sunt P.
- O~∃: Nu există S sau unii S nu sunt P10.
Pentru claritate: diferența dintre o propoziție categorică X, interpretată ca având supoziție existențială (X∃), și aceeași propoziție X, interpretată ca fiind fără supoziție existențială (X~∃) ține de condițiile în care este adevărată sau falsă. Astfel:
- X∃ este adevărată numai dacă subiectul său logic denotă obiecte care există; în cazul în care subiectul logic nu denotă niciun obiect, X∃ este falsă;
- X~∃ poate fi adevărată atât în cazul în care subiectul său logic denotă obiecte existente, cât și în cazul în care subiectul nu denotă niciun obiect. Mai mult, în cazul în care subiectul nu denotă niciun obiect, propoziția este adevărată11.
Ne putem îndrepta atenția, acum, asupra pătratului opoziției. Astfel, date fiind interpretările posibile de mai sus ale propozițiilor categorice, rezultă 24 = 16 posibilități în care ele pot să figureze într-un pătrat al opoziției12:
|
1 |
A∃ |
E∃ |
I∃ |
O∃ |
|
2 |
A∃ | E∃ | I∃ | O~∃ |
|
3 |
A∃ | E∃ | I~∃ | O∃ |
|
4 |
A∃ | E∃ | I~∃ | O~∃ |
|
5 |
A∃ | E~∃ | I∃ | O∃ |
|
6 |
A∃ | E~∃ | I∃ | O~∃ |
| 7 | A∃ | E~∃ | I~∃ | O∃ |
|
8 |
A∃ | E~∃ | I~∃ | O~∃ |
| 9 | A~∃ | E∃ | I∃ | O∃ |
|
10 |
A~∃ | E∃ | I∃ | O~∃ |
|
11 |
A~∃ | E∃ | I~∃ | O∃ |
|
12 |
A~∃ | E∃ | I~∃ | O~∃ |
|
13 |
A~∃ | E~∃ | I∃ | O∃ |
|
14 |
A~∃ | E~∃ | I∃ | O~∃ |
| 15 | A~∃ | E~∃ | I~∃ | O∃ |
|
16 |
A~∃ | E~∃ | I~∃ | O~∃ |
Continuând abordarea generală de până acum, putem întreba: care dintre cele 16 combinații posibile descrie un pătrat logic în care sunt păstrate toate relațiile de opoziție, așa cum sunt ele descrise în mod obișnuit? Este util, poate, să le amintesc aici pe acestea din urmă:
Date fiind două propoziții categorice X și Y:
- X și Y sunt contrare dacă nu pot fi adevărate împreună, dar e posibil să fie false împreună13. În pătratul logic, propozițiile universale sunt propoziții contrare.
- X și Y sunt subcontrare dacă nu pot fi false împreună, dar e posibil să fie adevărate împreună14. În pătratul logic, propozițiile particulare sunt propoziții subcontrare.
- X și Y sunt contradictorii dacă nu pot fi nici adevărate, nici false împreună15. În pătratul logic, există două perechi de propoziții contradictorii: propoziția universal-afirmativă și propoziția particular-negativă, respectiv propoziția universal-negativă și propoziția partivular-afirmativă.
- X și Y se află în raport de subalternare dacă una (să zicem, X) o implică logic pe cealaltă (Y)16. În pătratul logic, există două perechi de propoziții aflate în raport de subalternare: propoziția universal-afirmativă implică logic propoziția particular-afirmativă, iar propoziția universal-negativă implică logic propoziția particular-negativă.
În mod obișnuit, aceste raporturi logice sunt reprezentate cu ajutorul pătratului opoziției:
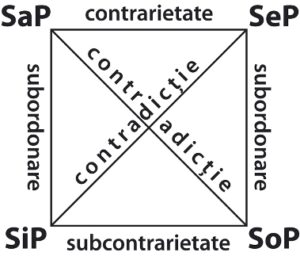
Putem reveni acum la întrebarea de mai sus: care dintre posibilitățile listate păstrează toate relațiile de opoziție din pătratul logic, așa cum sunt prezentate în mod obișnuit? Pentru scopurile de față, nu este necesar să le cercetăm pe toate. Așadar, mă voi concentra asupra celor două situații ce redau asumpțiile autorilor manualului pe care îl discutăm: situația (1) și situația (13)17.
Faptul că manualul atribuie propozițiilor categorice două seturi diferite de supoziții existențiale este, deja, un semn de alarmă că aparatul logic prezentat acolo este incoerent. Și, într-adevăr, vom vedea că așa stau lucrurile.
De unde știm ce supoziții existențiale sunt atribuite propozițiilor categorice?
Din două surse: din 1. reprezentarea grafică a propozițiilor categorice, respectiv din 2. catalogul inferențelor imediate considerate valide18.
În privința reprezentărilor grafice a propozițiilor categorice, manualul propune două astfel de metode: diagramele Euler și diagramele Venn. Acestea sunt juxtapuse ca și cum ar fi echivalente, ca și cum ar fi doar simple modalități alternative de a reprezenta aceleași conținuturi. Ele exprimă, însă, interpretări diferite ale propozițiilor categorice. Iar aceste diferențe privesc, desigur, tocmai supozițiile existențiale.
Să considerăm diagramele Euler. Particularitatea acestor diagrame este dată de următoarele:
- Extensiunea fiecărui termen al unei propoziții categorice este reprezentată printr-un cerc, iar poziția relativă a celor două cercuri reprezintă raportul logic dintre cei doi termeni pe care îl exprimă propoziția;
- Orice cade în afara extensiunii unui termen este considerat a fi (parte din) negația acelui termen. Cu alte cuvinte, diagramele Euler nu au capacitatea de a reprezenta situația în care un termen este vid (nu denotă niciun obiect).
Așadar, utilizarea diagramelor Euler pentru reprezentarea grafică a propozițiilor categorice atribuie supoziție existențială atât subiectului logic și predicatului logic, cât și contradictoriilor acestora19.
Voi reveni curând la diagramele Euler. Deocamdată, vom observa că „interpretarea Euler” are în comun cu situația (1) de mai sus faptul că atribuie supoziție existențială subiectului logic al unei propoziții categorice.
Să ne îndreptăm acum atenția asupra pătratului logic determinat de situația (1). Conform acesteia, toate cele patru forme ale propozițiilor categorice implică faptul că subiectul logic nu este vid. Sunt valabile, așadar, următoarele interpretări ale propozițiilor categorice:
- A∃: Există S și toți S sunt P.
- E∃: Există S și niciun S nu este P.
- I∃: Există S și unii S sunt P.
- O∃: Există S și unii S nu sunt P20.
Aceste asumpții nu păstrează, însă, relațiile de opoziție din pătratul logic. Mai precis, propozițiile categorice de cantitate și calitate opuse nu mai sunt contradictorii21.
Iată un exemplu: în timpul unei lecții, profesorul adresează elevilor câteva întrebări, iar niciun elev nu răspunde. Să considerăm acum propozițiile:
- Toate răspunsurile oferite de elevi sunt interesante.
- Unele răspunsuri oferite de elevi nu sunt interesante.
Conform teoriei prezentate în manual, cele două propoziții – una universal-afirmativă, iar cealaltă particular-negativă – sunt contradictorii: ele nu pot fi nici adevărate, nici false, împreună.
Conform supozițiilor existențiale discutate la acest punct, cele două propoziții trebuie înțelese astfel:
(1’) Există cel puțin un răspuns oferit de elevi și toate răspunsurile sunt interesante.
(2’) Există cel puțin un răspuns oferit de elevi care este neinteresant.
Dat fiind faptul că nu există niciun răspuns oferit de elevi, cele două propoziții sunt false. Deci, nu sunt contradictorii22.
Desigur, această concluzie este valabilă și pentru „interpretarea Euler”, în care este asumat caracterul nevid atât al subiectului logic și predicatului logic, cât și al contradictoriilor acestora23.
Interpretarea implicită în utilizarea diagramelor Euler este presupusă și în catalogul celorlalte inferențe imediate considerate valide. Problemele apar și aici. Iată un exemplu simplu:
Una dintre inferențele considerate valide este inversiunea parțială a propoziției universal-negative. Forma ei este următoarea:
Niciun S nu este P, deci unii non-S sunt P.
Ne amintim că o (schemă de) inferență este validă dacă și numai dacă nu este posibil ca premisele sale să fie adevărate, iar concluzia falsă. Prin urmare, dacă o schemă de inferență permite derivarea unei concluzii false din premise adevărate, atunci este nevalidă.
Să ne gândim acum la inversiunea parțială de mai sus.
Date fiind asumpțiile interpretării Euler, inferența este validă – fapt foarte simplu de verificat.
Dar, fie următorul argument:
- Niciun cetățean european nu a citit toate cărțile publicate în ultimii 1000 de ani.
- Prin urmare, unii cetățeni ne-europeni au citit toate cărțile publicate în ultimii 1000 de ani.
Premisa acestui argument este o propoziție adevărată, iar concluzia sa este o propoziție falsă (sper că această atribuire a valorilor de adevăr este evidentă pentru oricine). Rezultă că inversiunea parțială a unei propoziții universal-negative este o inferență nevalidă.
Am afirmat mai sus că, date fiind asumpțiile interpretării Euler, inferența este validă. Aplicat exemplului, acest lucru înseamnă că ar trebui să acceptăm că există, pe lângă cetățeni europeni și cetățeni ne-europeni, oameni care au citit toate cărțile publicate în ultimii 1000 ani. Contraexemplul scoate la iveală exact această asumpție problematică a interpretării Euler.
Așadar, contraexemplul de mai sus întărește argumentul ce avea în vedere doar relațiile din pătratul logic. Astfel, cele două argumente, împreună, arată inadecvarea celor două interpretări considerate până aici: interpretarea Euler și situația (1) din tabelul celor 16 posibilități. Pentru discuția noastră, importantă este, desigur, inadecvarea interpretării Euler a propozițiilor categorice.
În acest punct, avem următoarea concluzie intermediară:
(C1) Interpretarea propozițiilor categorice asumată implicit prin reprezentarea grafică a acestora cu ajutorul diagramelor Euler nu validează raporturile de opoziție dintre propozițiile categorice.
Putem trece acum la examinarea situației (13). În acest caz, propozițiile universale nu au supoziție existențială, iar cele particulare au. Aceasta este, de fapt, interpretarea modernă („booleană”) a propozițiilor categorice și este cea reprezentată în diagramele Venn, așa cum sunt ele prezentate în manual. Avem, așadar, următoarele interpretări:
- A∃: Nu există S sau toți S sunt P.
- E∃: Nu există S sau niciun S nu este P.
- I∃: Există S și unii S sunt P.
- O∃: Există S și unii S nu sunt P24.
Este binecunoscut faptul că interpretarea modernă a propozițiilor categorice modifică radical pătratul logic al opozițiilor: singurul raport logic ce rămâne valabil este raportul de contradicție. Pentru exemplificare, voi considera raportul de contrarietate.
Să considerăm, pentru exemplificare, un enunț pe care l-am considerat și mai devreme:
A~∃:Toți elevii ce au media semestrială la o disciplină mai mică de 5 sunt declarați corigenți la respectiva disciplină.
Am văzut că enunțul este adevărat și în situația în care nu există niciun elev care are media semestrială la o disciplină mai mică de 5.
Contrarul enunțului de mai sus este (sau ar trebui să fie, conform pătratului logic):
E~∃: Niciun elev cu media semestrială la o disciplină mai mică de 5 nu este declarat corigent la respectiva disciplină.
În interpretarea pe care o discutăm aici (cea modernă), acest enunț este tot adevărat în situația în care nu există niciun elev care are media semestrială la o disciplină mai mică de 525.
Așadar, în interpretarea asumată prin reprezentarea cu ajutorul diagramelor Venn, propozițiile universale pot fi adevărate simultan (când subiectul logic este un termen vid), de unde rezultă că nu sunt în raport de contrarietate.
Este interesant să notăm că, în interpretarea booleană asumată în reprezentarea cu ajutorul diagramelor Venn, inversiunea parțială a propoziției universal-negative este…nevalidă26.
Putem formula acum cea de a doua concluzie intermediară a discuției noastre:
(C2) Interpretarea propozițiilor categorice asumată implicit prin reprezentarea grafică a acestora cu ajutorul diagramelor Venn nu validează nici raporturile de opoziție din pătratul logic. De asemenea, mulțimea raporturilor de opoziție validate de interpretarea Venn și mulțimea raporturilor de opoziție validate de interpretarea Euler sunt diferite și incompatibile (interpretarea Venn păstrează contradicția, în timp ce interpretarea Euler, nu). Această situație este valabilă și în cazul celorlalte inferențe imediate (interpretarea Euler validează, de exemplu, conversiunea prin accident a propoziției universal-afirmative și inversiunea propoziției universal-negative, în timp ce interpretarea Venn, nu).
Putem desprinde acum următoarele concluzii primei secțiuni a lucrării, referitoare la aparatul conceptual prezentat în capitolul despre propozițiile categorice:
- Raporturile de opoziție din pătratul logic sunt definite în maniera obișnuită, dar supozițiile existențiale atribuite propozițiilor categorice nu validează toate aceste raporturi.
- Propozițiilor categorice le sunt atribuite supoziții existențiale diferite. Aceste supoziții existențiale sunt incompatibile, validând mulțimi diferite de inferențe. Am văzut acest lucru mai sus în privința raportului de contradicție și a unora dintre celelalte inferențe imediate. Același lucru ar fi putut fi demonstrat cu ușurință și în privința altor inferențe. Astfel, aparatul logic prezentat în manual este incoerent.
Desigur, întreaga analiză de mai sus poate fi extinsă la celelalte inferențe imediate cu propoziții categorice: conversiunea, obversiunea, contrapoziția, inversiunea. Și în acest caz, lucrurile stau asemănător ca mai sus: aceleași inferențe sunt și nu sunt validate, fără ca supozițiile existențiale să fie vreodată explicitate.
De asemenea, situația problematică poae fi întâlnită și în cazul tratamentului silogismului: pe de o parte, așa-numitele reguli generale ale silogismului validează moduri precum aai-3, în timp ce verificarea validității acestuia cu ajutorul diagramelor Venn îl arată ca fiind nevalid27. Avem, așadar, aceeași incoerență. Soluția oferită de autorii manualului este, de asemenea, complet nesatisfăcătoare. Însă, nu voi intra și în detaliile acestei discuții. Originea problemei este aceeași: înțelegerea confuză a propozițiilor categorice.
Voi încheia această primă secțiune prin menționarea și discutarea pe scurt a unei soluții posibile a problemei supoziției existențiale ce poate fi găsită în literatură, pe care nu am menționat-o până aici și care ar putea reprezenta o obiecție (parțială) la expunerea de față.
Discutând situația în care toate cele patru tipuri de propoziții categorice au supoziție existențială, J. N. Keynes explică astfel:
„Ar fi o problemă cu totul diferită dacă am asuma existența lui S și P independent de afirmația propoziției date. […]. Dar este în mod clar un lucru a spune (a) ”Toți S sunt P și S este presupus a exista”, și altul a spune (b) ”Toți S dunt P”, înțelegând prin aceasta ”S există și este întotdeauna P.” În cazul (a) este inutil a continua să facem supoziția că S este non-existent; în cazul (b), pe de altă parte, nu există nimic să ne împiedice să facem supoziția, și aflăm că, dacă este valabilă, propoziția dată este falsă.” (op. cit., p. 228, n. 1, traducerea mea, sublinierile în original)
Menționând pe scurt aceeași situație, W. E. Johnson scrie, la rândul său, explicitând un element important:
„O explicație specială este cerută pentru a justifica aplicarea termenilor contrar, contradictoriu, etc., în schema tradițională, unde toate cele patru propoziții generale sunt înțelese a asuma că există instanțe ale termenului-subiect. Această interpretare diferă de interpretarea (2)28 oferită mai sus, unde fiecare propoziție este interpretată drept conținând această afirmație; deoarece, în cazul în care nu ar exista nicio instanță a termenului-subiect, fiecare din cele patru forme de propoziție ar fi, conform schemei tradiționale, fără sens, în timp ce în interpretarea (2) ar fi false.” (op. cit., p. 139, traducerea mea, sublinierile în original)
Ideea fundamentală exprimată mai sus este următoarea: asertarea propozițiilor categorice presupune existența denotatului subiectului logic; iar dacă subiectul logic este vid, atunci propozițiile nu sunt (să zicem) false, ci nu sunt nici adevărate, nici false – adică, nu au valoare de adevăr. În perioada actuală, această propunere este asociată mai ales cu Peter Strawson29. În reacția pe care a avut-o30 la analiza logică a descripțiilor definite făcută de Bertrand Russell în articolul său epocal din 1905, „On Denoting”, Strawson a replicat că propoziția russelliană „Regele Franței este înțelept” nu implică „Există un rege al Franței”, ci presupune acest fapt. Prin urmare, dacă regele nu există, atunci „Regele Franței este înțelept” nu este falsă (așa cum cerea analiza lui Russell31), ci, pur și simplu, nu are valoare de adevăr. Astfel, conceptul de presupoziție conduce nu la o propoziție falsă, ci la o propoziție fără valoare de adevăr. Iar acest lucru face ca presupoziția să fie diferită de noțiunea de implicație, așa cum este aceasta înțeleasă în mod obișnuit. În această perspectivă, subalternarea, de exemplu, poate fi salvată. Cu alte cuvinte, dacă subiectul logic este vid, atunci pătratul nu este incorect, ci, mai degrabă, neadecvat, inaplicabil32.
Din fericire, nu este necesară discutarea în detaliu a acestei perspective, deoarece obiectivul principal pe care îl urmăresc aici este întemeierea acuzației de incoerență la adresa aparatului logic prezentat în manualul de logică – obiectiv independent de evaluarea perspectivei propuse de Strawson (sau Geach).
Pe de altă parte, însă, trebuie recunoscută relevanța perspectivei de mai sus pentru discuția privitoare la supoziția existențială a propozițiilor categorice: adoptarea soluției de mai sus înseamnă că există situații în care propozițiile categorice nu sunt nici adevărate, nici false. Or, asumpția discuției noastre a fost că o propoziție este adevărată sau falsă. Așadar, o scurtă discuție își are locul.
În primul rând, conceptul de presupoziție nu este atât de neproblematic sau atât de diferit de implicație pe cât ar putea să pară. Să presupunem că propoziția A presupune propoziția B. Cu alte cuvinte, A are valoare de adevăr numai dacă B este adevărată. Să asumăm mai departe că A este adevărată. Rezultă de aici, în mod banal, că A are valoare de adevăr. Avem, așadar: dacă A este adevărată, atunci A are valoare de adevăr. Dacă A are valoare de adevăr, atunci B este adevărată. Deci, prin tranzitivitatea implicației logice, dacă A este adevărată, atunci B este adevărată. Sau: dacă A o presupune pe B, atunci A o implică pe B33.
Fie A: „Regele Franței este înțelept”. A este adevărată dacă regele Franței este înțelept. Urmându-l pe Strawson, A o presupune pe B: există un unic rege al Franței. Conform argumentului de mai sus, propoziția „regele Franței este înțelept” implică „există un unic rege al Franței”.
Sau, fie A: „Toți S sunt P.” Conform lui Strawson, propoziția este adevărată numai dacă „există S” este adevărată34. Conform argumentului de mai sus, „Toți S sunt P” implică „există S”. Dar, exact așa se comportă propoziția noastră A∃35! Cu alte cuvinte, aparatul conceptual prezentat mai sus poate exprima exigențele impuse de perspectiva lui Strawson. Pe de altă parte, am pus deja în evidență consecințele atribuirii supoziției existențiale tuturor tipurilor de propoziții categorice.
Didactica logicii
În comparație cu discuția aspectelor științifice, secțiunea didactică va cuprinde o serie de observații, unele bazate pe experiența pe care o am ca profesor, altele bazate pe examinarea manualului.
Primul lucru pe care l-aș remarca este lipsa unei orientări bine definite a manualului: este un manual de logică formală sau este un manual de teoria argumentării. Distincția este foarte importantă: pe de o parte, ea întemeiază întregi domenii de cercetare, cu obiective și metode diferite (chiar dacă nu incompatibile); pe de altă parte, ca o consecință, ea poate determina întreaga structură a unui manual. Date fiind competențele specificate de programa analitică, probabil că orientarea cea mai potrivită este spre gândirea critică și teoria argumentării.
Manualul nu conține niciun indiciu privitor la competențele ce determină alegerea conținuturilor și a exercițiilor. Nici nu este deloc clar care este legătura dintre competențele umărite și conținuturile sau exercițiile prezentate. De exemplu, nu este deloc clară legătura dintre exercițiile din manual și competențe precum:
1. Utilizarea conceptelor specifice științelor sociale pentru organizarea demersurilor de cunoaștere și explicare a unor fapte, evenimente, procese din viața reală
2. Aplicarea cunoștințelor specifice științelor sociale în rezolvarea unor situații problemă, precum și în analizarea posibilităților personale de dezvoltare36
Așa cum înțeleg eu competențele menționate mai sus, ele conduc spre activități de învățare în care sunt puse în evidență utilizări „reale” ale conceptelor propuse. Să considerăm, de exemplu, capitolul despre definiții. Formarea competențelor de mai sus ar implica analizarea diferitelor tehnici de a defini, specifice diferitelor domenii ale cunoașterii, discutarea diferitelor tehnici de argumentare ce pornesc de la definiții (și clasificări), utilizarea sofistică a definițiilor etc.
Sau, să considerăm capitolul despre erorile de argumentare. Dincolo de o prezentare de un rând-două a fiecărei (presupuse) erori de argumentare, formarea competențelor de mai sus ar conduce către propunerea unor activități de învățare în care ar fi analizate situații unde un ad hominem, să zicem, este rezonabil sau ar fi propuse întrebări „critice” prin care astfel de argumente pot fi evaluate.
Exemplele pot fi înmulțite oricât. Desigur că astfel de activități cad în primul rând în sarcina profesorului și desigur că activitatea acestuia din urmă nu se reduce la ceea ce prezintă manualul. Însă, această observație nu anulează faptul că manualul nu propune nicio activitate de învățare care să conducă în mod real spre formarea competențelor cerute de programa școlară. Și desigur că discuția este mult mai largă. De exemplu, ne putem pune multe întrebări privitoare la locul logicii în planurile-cadru. Recunosc existența acestor probleme și a confuziei generale, la nivelul celor care alcătuiesc aceste planuri-cadru, privitoare la rostul și importanța deprinderii competențelor de argumentare și gândire critică. Logica este disciplina care a preocupat mințile multora dintre cele mai mari genii ale omenirii. În țara noastră, a fost la loc de cinste printre marii intelectuali români. Astăzi, ea este la loc de cinste în Occident. Este suficientă doar trecerea în revistă a cărților dedicate gândirii critice publicate. Dar este doar tolerată în învățământul românesc actual, redusă la un statut umilitor și degradant. Problemele manualului de logică, ca gen de carte, sunt independente (măcar parțial), însă, de aceste probleme mai generale (și, fără îndoială, foarte grave).
În sfârșit, dintr-un punct de vedere psihologic, ne putem întreba care este impactul motivațional pe care îl are manualul de logică asupra experienței de învățare a elevilor. cadrul teoretic ce mi se pare cel mai adecvat în acest scop este teoria auto-determinării („self-determination theory” sau SDT, de acum încolo), formulată inițial de către Richard Ryan și Edward Deci. Aceasta este, probabil, cea mai complexă teorie actuală a motivației – atât din punct de vedere teoretic, cât și al studiilor și aplicațiilor realizate.
SDT postulează existența a trei nevoi fundamentale ale oricărei persoane: competența, autonomia și relaționarea. Mai precis, pentru cazul elevilor:
- Competența este nevoia elevilor de a se simți capabili să se angajeze în procesul de învățare. Este necesar ca elevii să știe că munca lor îi conduce la realizarea completă a sarcinilor ce sunt importante pentru ei.
- Autonomia se referă la nevoia de a fi implicați în sarcini într-o manieră autonomă, într-un context ce este relevant pentru ei. Este necesar ca elevii să știe că se află la controlul propriilor acțiuni, că sarcinile față de care sunt angajați nu sunt dependente de prezența altora.
- Relaționarea privește nevoia de a fi implicați în realizarea unor sarcini ce presupun colaborarea și comunicarea cu alți elevi. Este necesar ca elevii să aibă un sentiment al apartenenței și al legăturii cu alte persoane în procesul de învățare.
Ne putem întreba: cum satisface manualul aceste nevoi? Răspunsul este, de asemenea, unul negativ.
Închei discuția prin menționarea a două fapte: în primul rând, trebuie spus că începutul schimbării în prezentarea logicii a existat. Într-adevăr, au existat două manuale realizate cu o viziune coerentă și în care orientarea spre gândirea critică și teoria argumentării este mult mai vizibilă, sau chiar definitorie. Într-o ordine cronologică, este vorba despre manualul realizat de Petre Bieltz și Mircea Dumitru37 și despre manualul realizat de Dragan Stoianovici și Ion Stepanescu[38]. Acest manual este orientat în întregime spre teoria argumentării, iar activitățile de învățare propuse vizează cu precizie formarea competențelor de argumentare, dezbatere, reflecție. Manualul este o provocare pentru profesori și elevi, deopotrivă, prin temele de reflecție propuse.
Nu este locul aici pentru a pune în evidență virtuțile sau eventualele neajunsuri ale acestor manuale, însă acestea pot fi verificate foarte ușor comparându-le cu manualul discutat aici.
În al doilea rând, este oportun să amintim și alte lucrări ale autorilor români în care problematica discutată aici este tratată foarte detaliat și riguros. Este adevărat că de data aceasta nu este vorba de manuale pentru liceu, ci de tratate de logică sau de manuale universitare; cred, însă, că menționarea lor este importantă pentru a contracara eventuala impresie greșită că logicienii români au fost străini de problematica discutată aici. Astfel, doresc să amintesc (în ordine cronologică a apariției) două expuneri excelente: în primul rând, monografia dedicată silogisticii de către Ion Didilescu și Petre Botezatu, (Didilescu & Botezatu, 1976), și bibliografia menționată acolo; în al doilea rând, aș menționa manualul universitar scris de Adrian Miroiu, (Miroiu, 1994), paragrafele 18, 20 și 21. Ambele aceste lucrări conțin expuneri și discuții excelente ale problematicii discutate aici, trecând cu mult dincolo de aceasta.
NOTE
1. O versiune în limba engleză, mai scurtă, a lucrării a fost prezentată în luna septembrie a acestui an la conferința internațională organizată de Universitatea Petrol-Gaze Ploiești, EDUCATION AND PSYCHOLOGY CHALLENGES – TEACHERS FOR THE KNOWLEDGE SOCIETY – 6th EDITION (EPC – TKS 2021) și va fi publicată în volumul de lucrări al conferinței. ↑
2. Voi elimina referirea la inferențele deductive: pe de o parte, nu este necesară; pe de altă parte, presupune că distincția dintre inferențele deductive și cele nedeductive este una clară și necontroversată – idee pe care înclin să o resping. Astfel, orice inferență poate fi evaluată în privința validității. ↑
3. Însă, este perfect posibil să avem inferențe valide cu premise și concluzie false sau inferențe valide cu premise false și concluzie adevărată. ↑
4. Pentru a nu îngreuna prezentarea, voi utiliza aparatul tehnic al logicii simbolice sau cel al teoriei mulțimilor doar în notele de subsol. Argumentarea poate fi înțeleasă și fără parcurgerea acestor note ceva mai tehnice. ↑
5. Formalizări standard:
– (∀x)(Sx→Px), adică: oricare ar fi obiectul x, dacă el are proprietatea S, atunci are proprietatea P;
– SP ̅=0, adică: mulțimea obiectelor care au proprietatea S și nu au proprietatea P este vidă. Trebuie observat că formalizările standard presupun, deja, atribuirea anumitor supoziții existențiale. Le prezint în acest punct doar cu scopul de a le introduce, pentru a ușura lectura celor pe care le voi prezenta mai jos, când voi discuta în detaliu atribuirea supozițiilor existențiale. Cu alte cuvinte, aceste formalizări redau adecvat forma logică a propozițiilor categorice numai acceptând o anumită atribuire a supozițiilor existențiale (pe care o vom discuta și noi, la timpul potrivit). Însă, tocmai modalitățile diferite în care pot fi înțelese (și, deci, formalizate) propozițiile categorice vor fi obiectul discuției ce va urma. ↑
6. Formalizări standard:
– (∀x)(Sx→~Px), adică: oricare ar fi obiectul x, dacă el are proprietatea S, atunci nu are proprietatea P;
– SP = 0, adică: mulțimea obiectelor care au proprietatea S și au proprietatea P este vidă. ↑
7. Formalizări standard:
– (∃x)(Sx & Px), adică: există cel puțin un obiect x care are proprietatea S și are proprietatea P;
– SP ≠ 0, adică: mulțimea obiectelor care au proprietatea S și au proprietatea P este nevidă. ↑
8. Formalizări standard:
– (∃x)(Sx & ~Px), adică: există cel puțin un obiect x care are proprietatea S și nu are proprietatea P;
– SP ̅ ≠ 0, adică: mulțimea obiectelor care au proprietatea S și au proprietatea P este nevidă. ↑
9. Pentru orice P ∈ {A,E,I,O}, vom avea următoarele situații:
a) P are supoziție existențială dacă există cel puțin un S. Simbolic, avem:
P∃ = df (∃x)Sx & P
În mod evident, orice propoziție ce are această formă implică (∃x)Sx.
b) P nu are supoziție existențială. Negarea supoziției existențiale trebuie înțeleasă drept o poziție neutră. Cu alte cuvinte, propozițiile înțelese astfel nu implică nici , nici . Cel mai natural mod de a exprima această idee este următoarea definiție:
P(∼∃) =df ∼(∃x)Sx ∨ P↑
10. Sau:
(1) A∃ :(∃x)Sx & (∀x)(Sx→Px);
(2) A~∃:~(∃x)Sx∨(∀x)(Sx→Px) sau, echivalent: (∀x)(Sx→Px);
(3) E∃ : (∃x)Sx & (∀x)(Sx→~Px);
(4) E~∃ :~(∃x)Sx ∨(∀x)(Sx→~Px) sau, echivalent: (∀x)(Sx→~Px);
(5) I∃: (∃x)Sx & (∃x)(Sx & Px) sau, echivalent: (∃x)(Sx & Px);
(6) I~∃ :~(∃x)Sx∨(∃x)(Sx & Px);
(7) O∃: (∃x)Sx & (∃x)(Sx & ~Px) sau, echivalent: (∃x)(Sx & ~Px)
(8) O~∃: ~(∃x)Sx∨(∃x)(Sx & ~Px).
Folosind și simbolismul teoriei mulțimilor, avem:
(1) A∃: S≠0 & SP ̅=0;
(2) A~∃: S = 0 ∨ SP ̅= 0 sau, echivalent: SP ̅= 0;
(3) E∃: S ≠ 0 & SP = 0;
(4) E~∃: S = 0 ∨ SP = 0 sau, echivalent: SP = 0;
(5) I∃: S ≠ 0 & SP ≠ 0 sau, simplificat: SP ≠ 0;
(6) I~∃: S = 0 ∨ SP ≠ 0;
(7) O∃: S ≠ 0 & SP ̅ ≠ 0 sau, simplificat: SP ̅ ≠ 0;
(8) O~∃: S = 0 ∨ SP ̅ ≠ 0.
Cu mici diferențe, formalizarea de mai sus a propozițiilor categorice în limbajul logicii predicatelor de ordinul I poate fi găsită, de asemenea, în (Chatti & Schang, 2013). De fapt, discuția aceasta poate fi găsită atât în (Keynes, 1906), cât și în primul volum (din trei) al cărții colaboratorului lui Keynes, (Johnson, 1921). Utilizarea limbajului simbolic are darul de a explicita forma logică a propozițiilor și, prin aceasta, de a face clare susținerile făcute. Menționez din nou, însă, parcurgerea acestor note tehnice nu este necesară pentru înțelegerea argumentării mele. ↑
11. Un exemplu poate face mai intuitivă această idee. Astfel, să ne gândim la următoare regulă școlară: „Toți elevii ce au media semestrială la o disciplină mai mică de 5 sunt declarați corigenți la respectiva disciplină.” Este o propoziție categorică universal-afirmativă adevărată. Ea este adevărată, desigur, dacă redă situația de fapt, adică dacă orice elev ce are media mai mică de 5 este corigent. Însă – foarte important pentru discuția noastră, ea rămâne adevărată și în situația în care subiectul logic – termenul „elevi ce au media semestrială la o disciplină mai mică de 5” – nu denotă niciun elev, adică în situația în care nu există niciun elev cu medii mai mici de 5. Cu alte cuvinte, interpretăm obișnuit această propoziție ca fiind fără supoziție existențială. ↑
12. Cf. (Chatti & Schang, 2013), p. 112. ↑
13. Sau: X și Y sunt contrare dacă ⊨~(X & Y). ↑
14. Sau: X și Y sunt subcontrare dacă ⊨X ∨ Y . ↑
15. Sau: X și Y sunt contradictorii dacă ⊨X W Y . ↑
16. Sau: X și Y se află în raport de subalternare dacă ⊨X→Y. ↑
17. Vom vedea că, de fapt, situația (1) redă asumpții mai slabe decât cele folosite de autorii manualului. Va fi suficient, însă, pentru a întemeia anumite concluzii. ↑
18. La pagina 39 a manualului, autorii prezintă sistematizarea inferențelor imediate valide (fără raporturile de opoziție) sub forma unui tabel pe care îl atribuie lui John Neville Keynes. Într-adevăr, tabelul poate fi găsit în tratatul de logică al acestui autor. De exemplu, în (Keynes, 1906), tabelul poate fi găsit la pagina 140. Mi pare notabil faptul că sursa exactă a tabelului nu este nicăieri menționată de autorii manualului. De asemenea, trebuie spus și că John Neville Keynes nu apare în bibliografia de la finalul cărții. ↑
19. Acest fapt l-am avut în vedere mai sus, la nota 16: față de „interpretarea Euler”, situația (1) atribuie supoziție existențială numai subiectului logic. ↑
20. Sau, formalizările următoare:
(1) A∃: S ≠ 0 & SP ̅ = 0;
(2) E∃: S ≠ 0 & SP = 0;
(3) I∃: S ≠ 0 & SP ≠ 0 sau, simplificat: SP ≠ 0;
(4) O∃: S ≠ 0 & SP ̅ ≠ 0 sau, simplificat: SP ̅ ≠ 0. ↑
21. Notând cu „W” operatorul disjuncției exclusive, avem următoarele situații:
a) ⊨A∃ W O∃:
⊨(S ≠ 0 & SP ̅= 0) W (S ≠ 0 & SP ̅ ≠ 0)
Se poate observa că disjuncția poate fi falsă: de exemplu, dacă S este vid, ambele conjuncții vor fi false. Cu alte cuvinte, A∃ și O∃ pot fi împreună false, ceea ce înseamnă că nu sunt contradictorii.
b) ⊨E∃ W I∃:
⊨(S ≠ 0 & SP = 0) W (S ≠ 0 & SP ≠ 0)
Din nou, în situația în care S este vid, ambele conjuncții sunt false, rezultând că E∃ și I∃ nu sunt propoziții contradictorii.
Concluzia ce se impune este: dacă propozițiile categorice atribuie supoziție existențială subiectului logic (situația (1) din cele 16 posibile), raportul de contradicție din pătratul logic nu se păstrează. ↑
22. Exemple de acest fel pot fi construite, desigur, și pentru cazul propozițiilor universal-negative, respectiv particular-afirmative. ↑
23. Din nou: diagramele Euler nu exprimă acele situații în care unul dintre termeni nu denotă niciun obiect. Voi avea ocazia să revin la acest aspect, în legătură cu o obiecție posibilă la argumentarea prezentată aici. ↑
24. Iar formalizările sunt următoarele:
(1) A~∃: S = 0 ∨ SP ̅= 0 sau, echivalent: SP ̅ = 0;
(2) E~∃: S = 0 ∨ SP = 0 sau, echivalent: SP = 0;
(3) I∃: S ≠ 0 & SP ≠ 0 sau, simplificat: SP ≠ 0;
(4) O∃ :S ≠ 0 & SP ̅ ≠ 0 sau, simplificat: SP ̅ ≠ 0. ↑
25. Un mod intuitiv de a înțelege acest lucru este să ne gândim că este echivalent cu enunțul „Nu există elevi cu media semestrială la o disciplină mai mică de 5 care sunt declarați corigenți” – enunț care este trivial adevărat în cazul în care nu există elevi cu media mai mică de 5. ↑
26. De fapt, nu este singura inferență nevalidă. În interpretarea modernă, orice inferență ce presupune derivarea unei concluzii particulare din premise universale (de exemplu, conversiunea prin accident a propoziției universal-afirmative) este nevalidă. ↑
27. În aceeași situație intră toate modurile silogistice în care premisele sunt propoziții universale, iar concluzia este o propoziție particulară. Rezultatul obținut prin aplicarea diagramelor Venn nu este deloc surprinzător: din propoziții fără supoziție existențială (cum sunt propozițiile universale, în interpretarea modernă – sau în situația noastră (13)) nu rezultă o propoziție ce are supoziție existențială (cum sunt propozițiile particulare, în aceeași interpretare). ↑
28. Adică, interpretarea în care toate cele patru forme ale propozițiilor categorice au supoziție existențială. ↑
29. Nu doar cu Peter Strawson. Un alt autor contemporan important ce a susținut o poziție asemănătoare este Peter Geach. A se vedea, de exemplu, (Geach, 1950), p. 480. ↑
30. Articolul lui Strawson, având titlul „On Referring”, a fost publicat în 1950, în revista Mind. Eu am folosit varianta republicată (Strawson, On Referring, 1996). ↑
31. Conform modului de analiză propus de Russell, propoziția „Regele Franței este înțelept” este echivalentă cu „Există un unic rege al Franței și acesta este înțelept”. În mod evident, dacă nu există regele Franței, atunci propoziția este falsă. ↑
32. Câteva observații pot aduce clarificări suplimentare. Conform lui Strawson, o expresie (concept sau enunț) nu se referă la nimic, prin ea însăși. Referirea este un act de folosire a expresiei. Același lucru trebuie spus și despre valoarea de adevăr a unui enunț: un enunț este adevărat atunci când este utilizat într-un anumit context pentru a realiza o aserțiune adevărată. Iar dacă enunțul nu este folosit pentru a realiza referința, atunci aceasta este o pseudo-utilizare: nu este realizată o aserțiune adevărată sau falsă. Prin urmare, problema valorii de adevăr nu se pune. Mutatis mutandis, folosirea unei propoziții categorice presupune că există acele lucruri denotate de subiectul logic. Dacă subiectul logic este un termen vid, atunci propoziția categorică nu poate fi nici adevărată, nici falsă. Neavând valoare de adevăr, utilizarea inferențelor din pătratul logic nu își are locul. Strawson susține exact această poziție în capitolul 6 al manualul său de logică, (Strawson, 1952/2011). ↑
33. Argumentul îi aparține lui B. Linsky (citat în (Chatti & Schang, 2013), p. 107). ↑
34. „Gândiți-vă că cineva spune ’Toți copiii lui John au adormit’. Evident, nu va spune aceasta în mod normal, sau corect, decât dacă este convins că John are copii (care au adormit). Dar să presupunem că greșește. Să presupunem că John nu are copii. Atunci este adevărat sau fals că toți copiii lui John au adormit? Fiecare din răspunsuri ar părea înșelător. Dar nu suntem constrânși să dăm niciun din răspunsuri. Putem, și în mod normal ar trebui, să spunem că, deoarece John nu are niciun copil, întrebarea nu apare. […]
Perspectiva mai realistă pare a fi aceea că existența copiilor lui John este o precondiție necesară nu doar a adevărului a ceea ce este spus, ci a faptului de a fi fie adevărat, fie fals. Iar acest lucru sugerează posibilitatea interpretării tuturor celor patru forme aristotelice pe aceste direcții: adică, drept forme astfel încât întrebarea dacă aserțiunile ce le exemplifică sunt adevărate sau false este ce nu apare decât dacă clasa-subiect are membri.” (Strawson, 1952/2011), pp. 173 și urm., traducerea mea, sublinierile în original. ↑
35. A se vedea, de asemenea, (Kleene, 1967), p. 140. ↑
36. Programă școlară Logică, argumentare și comunicare clasa a IX-a ciclul inferior al liceului, 2009, p. 4. ↑
37. A se vedea (Bieltz & Dumitru, 1999). De remarcat este începutul manualului, ce conține elemente ce vor fi publicate de logicianul American Richard Epstein în tratatul său de gândire critică (lucru menționat și de autorii manualului). De asemenea, este de remarcat (prin raportare la cele discutate aici) unitatea mult mai pronunțată a tratamentului propozițiilor categorice și a silogismelor. De asemenea, prezentarea conținuturilor este mult mai nuanțată și, prin aceasta, mai „realistă”, reflectând opțiunile teoretice ale autorilor, precum și viziunea bine definită. ↑
38. A se vedea (Stoianovici & Stepanescu, 2001). Acest manual este orientat în întregime spre teoria argumentării, iar activitățile de învățare propuse vizează cu precizie formarea competențelor de argumentare, dezbatere, reflecție. Manualul este o provocare pentru profesori și elevi, deopotrivă, prin temele de reflecție propuse. ↑
BIBLIOGRAFIE
Bieltz, P., & Dumitru, M. (1999). Logică și argumentare. Manual pentru clasa a 9-a. București: ALL Educațional.
Chatti, S., & Schang, F. (2013). The Cube, the Square, and the Problem of Existential Import. History and Philosophy of Logic, 34(2), 101-132.
Didilescu, I., & Botezatu, P. (1976). Silogistica. Teoria clasică și interpretările moderne. București: Editura didactică și pedagogică.
Geach, P. T. (1950). Subject and Predicate. Mind, 59(236), 461-482.
Johnson, W. E. (1921). Logic. Cambridge: Cambridge University Press.
Keynes, J. N. (1906). Studies and Exercises in Formal Logic (ed. 4th). London: MACMILLAN AND CO., Limited.
Kleene, S. C. (1967). Mathematical Logic. Mineola: Dover Publications, Inc.
Lupșa, E., Bratu, V., & Stoica, M. D. (2004). Logică și argumentare. Manual pentru clasa a IX-a. Deva: Editura Corvin.
Miroiu, A. (1994). Introducre în logica filosofică. București: Editura Universității București.
Stoianovici, D., & Stepanescu, I. (2001). Logică și argumentare. Manual pentru clasa a IX-a. București: Sigma.
Strawson, P. F. (1952/2011). Introduction to Logical Theory. New York: Routledge.
Strawson, P. F. (1996). On Referring. În A. P. Martinich, The Philosophy of Language (pg. 215-230). New York: Oxford University Press.


In topul motivelor pentru care elevul/studentul invata se afla mediul din familie si profesorul.
Manualul scolar este pe locul 5-6. Rolul lui nici macar nu este important in tot procesul de invatare. Asta ne spune cercetarea aplicata.
Problema la noi in tara este ca politicienii folosesc manualul scolar pentru a manipula opinia publica. Este mai usor si mai ieftin sa refaci niste carti (prin Ministerul Educatiei) decat sa investesti in protectie sociala sau in pregatirea cadrelor didactice. Beneficiile unui astfel
de demers se vad in cel putin cateva decenii. Iar pe politicieni nu-i intereseaza perspectiva din educatie, ci doar sa manipuleze pentru a mai beneficia de inca un mandat. Dupa aceea… mai vad ei. Se descurca!